¿��Ĺ������Stein��GCD��Ȥ�
| �ץ�������� | 2012/04/22 Sun 22:43
���Τ褦�ʡ�32bit�Ϥ�¿��Ĺ�������饹�����ä��Ȥ��ơ�
16�ʤǼ��Τ褦��ɽ���������������
0x111100002222000033330000
���Υ��饹�Ǥϼ��Τ褦�˳�Ǽ������ΤȤ��롣(��1)
������Ѥ��ơ�Stein's algorithm�ˤ��GCD����ͤ��롣
Stein��GCD�ˤĤ��Ƥ�WikiPedia���ܤ�����
http://en.wikipedia.org/wiki/Binary_GCD_algorithm
���̤� �桼����åɤθ߽�ˡ(��ĥ) �������롼�ײ���Ͼ��ʤ�����
��;�����ͥå��ˤʤꡢ�������������ʤ��礬¿����
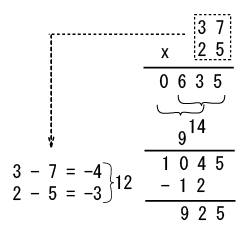
â������������軻����;���Υ��르�ꥺ�����ͤη���ˤ�äƤϡ�
�롼�ײ���ξ��ʤ��桼����åɤθ߽�ˡ(��ĥ)�������ᤤ���⤢�롣
Stein�Υ��르�ꥺ����٤��Ȼפ���Τϡ�Shift�黻�β���˿Ԥ��롣
����ץ륳���ɤΤޤȤ��ȡ���������٤ξ��ʤ�Shift�黻�ȸ����ɤ⡢
¿��黻�ǽ��������¿���ʤ���礭���ٱ���ޤ���
WikiPedia��Stein�Υ���ץ륳���ɤ�����Ȥʤ�Τϡ�
����ʬ���פϱ�ü�Σ������Ƥ�������Ǥ��롣
��ü���¤�Ǥ��룰�ο��������ؿ����Ѱդ��ơ�Shift����餳�Ȥ��ܻؤ���
http://en.wikipedia.org/wiki/Count_trailing_zeros �ˤ⤢�뤬��
intel�ϤǤ���С�������֥�(bsf)���Ȥ��롣
BITPERBLOCK�ϡ����Ĥ˴ޤޤ��¿��Ĺ������Bit���Ǥ��롣
32bit�Ǥ���С�32���Ȥ����礬¿����(��2)
(64bit�ξ�硢bsfq��Ȥ���)
(m_sz=2, BITPERBLOCK=32)�μ��Τ褦��¿��Ĺ����������Ȥ�
������֥��Ȥ�ʤ�������ˡ�⤢�롣
http://en.wikipedia.org/wiki/Count_trailing_zeros �ˤ⤢��ޤ�����
�ͷ����Ȥä��ޥ��å��Ǥ���
������������ܤ����Ǥ��� http://d.hatena.ne.jp/siokoshou/20090704
����ȡ�Stein�Υ����ɤϼ��Τ褦�˽롣
�����30��40%�ϡ��������֤�û�̤Ǥ��ޤ�����
���줳����Steins;Gate�������
���Υ����ɤ������������ץ��16�ʡ����ʡ�10������Ǥ���
���������Ǥ������褽100����ޤǷ��Ǥ��ޤ���

(��1) ����Ĺ�ǤϤʤ�Bigint���饹�Ǥϡ���Ĺ���������Υ���δ�����ɬ�פˤʤ�Τǡ�����ۤ�ñ��ʤ�ΤǤϤ���ޤ���
(��2) 32bit(Block)���Ƥ�Ȥ����Ȥ�ɬ������ͭ���ǤϤ���ޤ���SSE��ͭ���˻Ȥ��ʤ�夢�դ줬ȯ�����ʤ��褦 31bit �ʲ��ˤ��ޤ���
Tags: �ץ��������
class Bigint { public: Bigint(); ... ... �͡������(��§�黻��operator=,operator<<=��) ... private: int m_sz; // ����� int* m_num; // ����(��ȥ륨��ǥ�����) };
16�ʤǼ��Τ褦��ɽ���������������
0x111100002222000033330000
���Υ��饹�Ǥϼ��Τ褦�˳�Ǽ������ΤȤ��롣(��1)
(m_sz=3) |- m_num[0]-|- m_num[1]-|- m_num[2]-| | 3333 0000 | 2222 0000 | 1111 0000 |
������Ѥ��ơ�Stein's algorithm�ˤ��GCD����ͤ��롣
Stein��GCD�ˤĤ��Ƥ�WikiPedia���ܤ�����
http://en.wikipedia.org/wiki/Binary_GCD_algorithm
���̤� �桼����åɤθ߽�ˡ(��ĥ) �������롼�ײ���Ͼ��ʤ�����
��;�����ͥå��ˤʤꡢ�������������ʤ��礬¿����
â������������軻����;���Υ��르�ꥺ�����ͤη���ˤ�äƤϡ�
�롼�ײ���ξ��ʤ��桼����åɤθ߽�ˡ(��ĥ)�������ᤤ���⤢�롣
Stein�Υ��르�ꥺ����٤��Ȼפ���Τϡ�Shift�黻�β���˿Ԥ��롣
����ץ륳���ɤΤޤȤ��ȡ���������٤ξ��ʤ�Shift�黻�ȸ����ɤ⡢
¿��黻�ǽ��������¿���ʤ���礭���ٱ���ޤ���
WikiPedia��Stein�Υ���ץ륳���ɤ�����Ȥʤ�Τϡ�
/* From here on, u is always odd. */ do { while ((v & 1) == 0) /* Loop X */ v >>= 1;
����ʬ���פϱ�ü�Σ������Ƥ�������Ǥ��롣
��ü���¤�Ǥ��룰�ο��������ؿ����Ѱդ��ơ�Shift����餳�Ȥ��ܻؤ���
http://en.wikipedia.org/wiki/Count_trailing_zeros �ˤ⤢�뤬��
intel�ϤǤ���С�������֥�(bsf)���Ȥ��롣
// // ��®���Τ���������å���ԤäƤ��ʤ� // �������ȥ���������ȿ���㳰�� // int Bigint::bsf() const{ int* p = m_num; __asm{ mov edx, [p] mov eax, edx bsf_l2: bsf ecx, [eax] jnz bsf_l1 add eax, 4 jmp bsf_l2 bsf_l1: sub eax, edx shr eax, 2 mov edx, BITPERBLOCK mul edx add eax, ecx } }
BITPERBLOCK�ϡ����Ĥ˴ޤޤ��¿��Ĺ������Bit���Ǥ��롣
32bit�Ǥ���С�32���Ȥ����礬¿����(��2)
(64bit�ξ�硢bsfq��Ȥ���)
(m_sz=2, BITPERBLOCK=32)�μ��Τ褦��¿��Ĺ����������Ȥ�
bsf()�ϡ�32+16=48 ���֤���|- m_num[0]-|- m_num[1]-| | 0000 0000 | ABCD 0000 |
������֥��Ȥ�ʤ�������ˡ�⤢�롣
int Bigint::bsf() const{ static int table[32] = {0,1,10,2,11,14,22,3,30,12,15,17,19,23,26,4,31,9,13,21,29,16,18,25,8,20,28,24,7,27,6,5}; int count = 0; for (int i=0; i<m_sz; i++){ int x = m_num[i]; if (x == 0){ count += BITPERBLOCK; }else{ count += table[((unsigned int)(x & -x) * 0x07C4ACDDUL) >> 27]; break; } } return count; } // 64bit/Block�� int Bigint::bsf64() const{ static int table[64] = { 0,1,59,2,60,40,54,3,61,32,49,41,55,19,35,4,62,52,30,33,50,12,14,42,56,16,27,20,36,23,44,5, 63,58,39,53,31,48,18,34,51,29,11,13,15,26,22,43,57,38,47,17,28,10,25,21,37,46,9,24,45,8,7,6}; int count = 0; for (int i=0; i<m_sz; i++){ __int64 x = m_num[i]; if (x == 0){ count += BITPERBLOCK; }else{ count += table[((unsigned __int64)(x & -x) * 0x03F566ED27179461ULL) >> 58]; break; } } return count; }
http://en.wikipedia.org/wiki/Count_trailing_zeros �ˤ⤢��ޤ�����
�ͷ����Ȥä��ޥ��å��Ǥ���
������������ܤ����Ǥ��� http://d.hatena.ne.jp/siokoshou/20090704
����ȡ�Stein�Υ����ɤϼ��Τ褦�˽롣
// // *this = GCD(*this, v) // void Bigint::gcd(const Bigint& v) { if (v == 0){ return; } if (operator==(0)){ operator= (v); return; } Bigint x[2] = {*this, v}; if (x[0] < 0) x[0].operator-(); if (x[1] < 0) x[1].operator-(); int i0 = x[0].bsf(); int i1 = x[1].bsf(); int shift = (i0 < i1) ? i0 : i1; x[0] >>= i0; x[1] >>= shift; int id = 0; do { x[id^1] >>= x[id^1].bsf(); if (x[id] > x[id^1]){ id ^= 1; } x[id^1] -= x[id]; } while (x[id^1] != 0); operator= (x[id] << shift); }
�����30��40%�ϡ��������֤�û�̤Ǥ��ޤ�����
���줳����Steins;Gate�������
���Υ����ɤ������������ץ��16�ʡ����ʡ�10������Ǥ���
���������Ǥ������褽100����ޤǷ��Ǥ��ޤ���
(��1) ����Ĺ�ǤϤʤ�Bigint���饹�Ǥϡ���Ĺ���������Υ���δ�����ɬ�פˤʤ�Τǡ�����ۤ�ñ��ʤ�ΤǤϤ���ޤ���
(��2) 32bit(Block)���Ƥ�Ȥ����Ȥ�ɬ������ͭ���ǤϤ���ޤ���SSE��ͭ���˻Ȥ��ʤ�夢�դ줬ȯ�����ʤ��褦 31bit �ʲ��ˤ��ޤ���
Tags: �ץ��������
author : HUNDREDSOFT | - | -