JavascriptЄЧКйРўВН
| ЅзЅэЅАЅщЅрЅсЅт | 2013/10/19 Sat 21:49
ЃВУЭВНВшСќЄЮЅщЅЄЅѓЄђКйРўВНЄЙЄыЅЂЅыЅДЅъЅКЅрЄЯТєЛГЄЂЄъЄоЄЙЄЌЁЂ
ЅыЁМЅзВѓПєЄЌЄЩЄІЄЗЄЦЄтТПЄЏЄЪЄыЄЮЄЧЁЂjavascriptЄЧЄЮМТСѕЮуЄЯОЏЄЪЄЄЄЧЄЙЁЃ
ЄГЄГЄЧЄЯЁЂШцГгХЊЙтТЎЄЪZhang-Suen, NWGЄШЁЂХФТМЄЮЪ§МАЄђМТСѕЄЗЄЦЄпЄоЄЙЁЃ
МТЙдЅЕЅѓЅзЅыЄЯЄГЄСЄщ
Zhang-SuenЄЮЅЂЅыЅДЅъЅКЅрЄЯЁЂШцГгХЊУБНуЄЧЄЂЄыЄЮЄЧМТСѕЄЗАзЄЄЄЧЄЙЁЃ
ЅщЅЙЅПЅЙЅЅуЅѓЄЫЄшЄъВшСЧО№ЪѓЄђЦЩЄпЙўЄпЁЂ
ФДККВшСЧЄђДоЄрЁЂ3x3pixЄЮВшСЧУЭЄЫТаЄЗЁЂ3МяЄЮОђЗяЄђЫўЄПЄЗЄЦЄЄЄьЄаЁЂ
ФДККВшСЧЄђЧђ(1)ЄЋЄщЙѕ(0)ЄЫУжЄДЙЄЈЄоЄЙЁЃ
ФДККВшСЧ(P1)ЄђДоЄрЁЂ3x3pixЄЮВшСЧЄЫМЁЄЮЄшЄІЄЫШжЙцЄђПЖЄыЁЃ
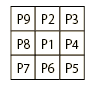
ОђЗяЃБЁЅ
ОђЗяЃВЁЅ
ОђЗяЃГ(1)ЁЅ
ОђЗяЃГ(2)ЁЅ
ЄоЄКЁЂОђЗяЃБЁЅЃВЁЅЃГ(1)ЄЮШНФъЄђЙдЄЄЁЂОђЗяЄђЫўЄПЄЗЄПОьЙчЁЂГКХіВшСЧЄђНќЕюЅъЅЙЅШЄЫФЩВУЄЙЄыЁЃ
СДВшСЧФДККИхЁЂНќЕюЅъЅЙЅШЄЫВшСЧЄЌЄЂЄьЄаЁЂЄНЄЮВшСЧЄђСДЄЦЙѕ(0)ЄЫЪбЄЈЄыЁЃЄЪЄБЄьЄаНЊЮЛЄЙЄыЁЃ
МЁЄЫЁЂОђЗяЃБЁЅЃВЁЅЃГ(2)ЄЮШНФъЄђЙдЄЄЁЂЦБЭЭЄЮНшЭ§ЄђТГЄБЄыЁЃ
АЪЙпЁЂОђЗяЃГ(1)(2)ЄђРкЄъТиЄЈЄЪЄЌЄщЁЂОђЗяЄђЫўЄПЄЙВшСЧЄЌЄЪЄЏЄЪЄыЄоЄЧЁЂЗЋЄъЪжЄЗЙдЄІЁЃ
NWG (Nagendraprasad-Wang-Gupta)ЄЫЄФЄЄЄЦ ЄЯЁЂZhang-SuenЄШШѓОяЄЫЛїЄПНшЭ§ЄЧЄЂЄыЄПЄсЁЂ
РтЬРЄЯГфАІЄЗЄоЄЙЁЃ
ОмКйЄЯЁЂЅНЁМЅЙЅГЁМЅЩЄЋЁЂ
A note on the Nagendraprasad-Wang-Gupta thinning algorithm ЄђЄДЭїЄЏЄРЄЕЄЄЁЃ
Zhang-SuenЄЮЅЂЅыЅДЅъЅКЅрЄЌМчЄЫЗзЛЛЄЫЄшЄыШНФъЄђЙдЄІЄЮЄЫТаЄЗЁЂ
ХФТМЄЮЅЂЅыЅДЅъЅКЅрЄЯЁЂПоЗСЄЮЅоЅУЅСЅѓЅАЄђЭјЭбЄЗЄоЄЙЁЃ
ТчЄоЄЋЄЪНшЭ§ЄШЄЗЄЦЄЯЁЂ
2МяЮрЄЮЅбЅПЁМЅѓЄЌЄЂЄъЁЂЄНЄьЄОЄьЄЮЅбЅПЁМЅѓЄЯЁЂ
3x3ЄЮНќЕюЅбЅПЁМЅѓЄШ3x3ЄЮШѓНќЕюЅбЅПЁМЅѓЄЫЪЌЄЋЄьЄыЁЃ
ЁЪЄГЄГЄЧИРЄІНќЕюЄЯЁЂЧђЄЋЄщЙѕЄиЄЮЪбЙЙЄђАеЬЃЄЙЄыЁЃЁЫ
ЅщЅЙЅПЅЙЅЅуЅѓЄЫЄшЄъВшСЧО№ЪѓЄђЦЩЄпЙўЄпЁЂ
ГЦВшСЧЄЫЄФЄЄЄЦ3x3ЄЮЅбЅПЁМЅѓЅоЅУЅСЅѓЅАЄђЙдЄІЁЃ
ЅбЅПЁМЅѓЄЫЄЯМЁЄЮЄтЄЮЄЌЄЂЄыЁЃ
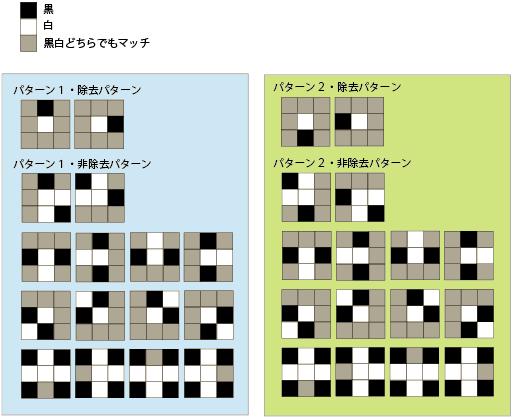
ЁкНшЭ§ГЕЭзЁл
Ё ЅбЅПЁМЅѓЃБЄЮНќЕюЅбЅПЁМЅѓЄЧЅоЅУЅСЅѓЅАЄЙЄьЄаЂЄиЁЂАьУзЄЗЄЪЄБЄьЄаМЁВшСЧЄиЁЃ
Ђ ЅбЅПЁМЅѓЃБЄЮШѓНќЕюЅбЅПЁМЅѓЄЧЅоЅУЅСЅѓЅАЄЙЄьЄаМЁВшСЧЄиЁЂАьУзЄЗЄЪЄБЄьЄаЃЄиЁЃ
Ѓ ГКХіВшСЧЄђНќЕюЅъЅЙЅШЄЫФЩВУЄЗЁЂМЁВшСЧЄиЁЃ
Є ЁЁСЃЄЮНшЭ§ЄђСДВшСЧЄЫТаЄЗЄЦЙдЄІЁЃ
Ѕ НќЕюЅъЅЙЅШЄЫВшСЧЄЌЄЂЄьЄаЁЂЄНЄЮВшСЧЄђСДЄЦЙѕ(0)ЄЫЪбЄЈЄыЁЃЄЪЄБЄьЄаНЊЮЛЁЃ
І ЅбЅПЁМЅѓЃВЄЮНќЕюЅбЅПЁМЅѓЄЧЅоЅУЅСЅѓЅАЄЙЄьЄаЇЄиЁЂАьУзЄЗЄЪЄБЄьЄаМЁВшСЧЄиЁЃ
Ї ЅбЅПЁМЅѓЃВЄЮШѓНќЕюЅбЅПЁМЅѓЄЧЅоЅУЅСЅѓЅАЄЙЄьЄаМЁВшСЧЄиЁЂАьУзЄЗЄЪЄБЄьЄаЈЄиЁЃ
Ј ГКХіВшСЧЄђНќЕюЅъЅЙЅШЄЫФЩВУЄЗЁЂМЁВшСЧЄиЁЃ
Љ ІЁСЈЄЮНшЭ§ЄђСДВшСЧЄЫТаЄЗЄЦЙдЄІЁЃ
Њ НќЕюЅъЅЙЅШЄЫВшСЧЄЌЄЂЄьЄаЁЂЄНЄЮВшСЧЄђСДЄЦЙѕ(0)ЄЫЪбЄЈЄыЁЃЄЪЄБЄьЄаНЊЮЛЁЃ
Ћ ЁЄЫЬсЄыЁЃ
ЁкЅоЅУЅСЅѓЅАЅГЁМЅЩЮуЁл
РтЬРЄЮАйЄЫЁЂ3x3pixЄЧЩНИНЄЕЄьЄыЃБЄФЄЮЅбЅПЁМЅѓЄЫP0ЁСP8ЄЮШжЙцЄђПЖЄъЄоЄЙЁЃ
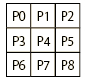
P0ЁСP8ЄђГЦ2bitЄЧЩНЄЙЄтЄЮЄШЄЗЁЂ
Чђbit:10, Йѕbit:01, ЄЩЄСЄщЄЧЄтЮЩЄЄЄтЄЮЄЯbit:00ЁЁЄШЄЗЄоЄЙЁЃ
ГЦЮѓЄЮРшЦЌ2bitЄЫ00ЄђЩеВУЄЗЁЂЃБЅаЅЄЅШ/ЮѓЄЧЩНИНЄЙЄыЄШЁЂ
ЃБЅбЅПЁМЅѓЄЯЃГЅаЅЄЅШЄЫЄЪЄъЄоЄЙЁЃ
ЮуЄЈЄаЁЂЅбЅПЁМЅѓЃБЄЮНќЕюЅбЅПЁМЅѓЄЧЄЂЄьЄаЁЂ
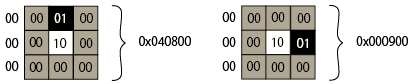
ЄГЄГЄЧЁЂЄЂЄыВшСЧЄђДоЄр3x3pixЄЮОѕТжЄЌМЁЄЮЭЭЄЫЄЪЄУЄЦЄЄЄыЄШЄЙЄыЄШ
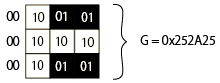
ЄГЄьЄЯЁЂЅбЅПЁМЅѓЃБЁІШѓНќЕюЅбЅПЁМЅѓЄЮ6ШжЬмЄШЅоЅУЅСЄЗЄоЄЙЁЃ
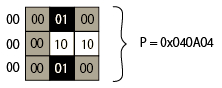
ШѓНќЕюЅбЅПЁМЅѓ(6)ЄЯЁЂP = 0x040A04ЄЧЩНИНЄЕЄьЄыЄЮЄЧ
G AND P = P ЄЌРЎЄъЮЉЄФЁЃ
ЄГЄЮЯРЭ§МАЄЌРЎЄъЮЉЄФОьЙчЄЫЁЂЅбЅПЁМЅѓЅоЅУЅСЄШЧЇФъЄЧЄЄоЄЙЁЃ
ХФТМЄЮЪ§МАЄЧЄЯЁЂЄНЄьЄлЄЩЅбЅПЁМЅѓЄЌТПЄЏЄЪЄЄЄЮЄЧЁЂ
ГфЄШДЪУБЄЪЅГЁМЅЧЅЃЅѓЅАЄЧКбЄпЄоЄЙЁЃ
РтЬРЄЧЄЯКяНќЅъЅЙЅШЄђЛШЄУЄЦЄЄЄоЄЙЄЌЁЂИЕЅЧЁМЅПЄђTypedArray(Uint8Array)ЄЫЅГЅдЁМЄЗЄПЪ§ЄЌСсЄЋЄУЄПЄЮЄЧЁЂ
МТСѕЄЧЄЯЁЂЪбЄЈЄЦЄЄЄоЄЙЁЃ(ЦтЭЦХЊЄЫЪбЄяЄыЄтЄЮЄЧЄЯЄЂЄъЄоЄЛЄѓЁЃ)
Zhang-Suen,NWG,ХФТМЄЧЁЂЄЩЄЮЪ§ЫЁЄЌЮЩЄЄЄЋЄЯЁЂЦўЮЯВшСќЄЫЄшЄУЄЦЪбЄяЄыЄЮЄЧАьГЕЄЫЄЯИРЄЈЄоЄЛЄѓЁЃ
ЅЕЅѓЅзЅыЄђЦАЄЋЄЙЄШЄяЄЋЄъЄоЄЙЄЌЁЂНшЭ§ЛўДжЄЫДиЄЗЄЦЄЯЁЂNWGЄшЄъЁЂZhang-SuenЄЮЪ§ЄЌСсЄЄЄЧЄЙЁЃ
NWGЄЯЁЂZhang-SuenЄЮВўЮЩШЧЄЧЄЂЄыЄПЄсМуДГНшЭ§ЄЌС§ЄЈЄЦЄЄЄыЄПЄсЄЧЄЙЁЃ
ПЭДжЄЮЬмЄЧИЋЄыЄШЖЯЄЋЄЪАуЄЄЄЧЄЙЄЌЁЂNWGЄЮЪ§ЄЌхКЮяЄЫЄЪЄУЄЦЄЄЄыЄшЄІЄЧЄЙЁЃ
ХФТМЄЫДиЄЗЄЦЄЯЁЂЅЕЅѓЅзЅыЄЮВшСќЃБЁІВшСќЃВЄЧЄЯТЎХйЄЌЮєЄъЄоЄЙЄЌЁЂВшСќЃГЄЧЄЯАЕХнХЊЄЫСсЄЄЄЧЄЙЁЃ
ЪИЛњЗЯЄЧЄЯЬЏЄЪЄвЄВЄЌНаЄфЄЙЄЄЄЧЄЙЄЌЁЂМЬППХљЄЮЅЈЅУЅИУъНаВшСќЄЫТаЄЗЄЦЄЯЮЩЄЄЗыВЬЄЌНаЄЦЄЄЄоЄЙЁЃ
(ЯРЪИШЏЩННчЄЧЄЯЁЂЁкHilditch(1968)ЁлЂЊЁкХФТМ(1978)ЁлЂЊЁкZhang-Suen(1984)ЁлЂЊЁкNWG(1989)Ёл)
КЃВѓМТСѕЄЗЄЦЄЄЄоЄЛЄѓЄЌЁЂ
HilditchЄЮЪ§ЫЁЄЯКйРўВННшЭ§ЄЮИЕСФЄШЄтИРЄЈЄоЄЙЄЌЁЂННЪЌЄЪЗыВЬЄЌЦРЄщЄьЄЪЄЄОьЙчЄЌЄЂЄыЄщЄЗЄЄЁЃ
RosenfeldЄЯЁЂZhang-Suen,NWG,ХФТМЄЫШцЄйЁЂЄЋЄЪЄъНшЭ§ЄЌНХЄЏЄЪЄыЄщЄЗЄЄЁЃ
ЁЪЛВЙЭЁЇ Comparing Hilditch, Rosenfeld, Zhang-Suen,and Nagendraprasad - Wang-Gupta Thinning ЁЫ
МТЙдЅЕЅѓЅзЅыЄЯЄГЄСЄщ
IE10/Chrome/FF/AndroidЄЧЁЂГЮЧЇЄЗЄЦЄЄЄоЄЙЁЃ
IE9ЄЯЁЂTypedArray(Uint8Array)ЄЫТаБўЄЗЄЦЄЄЄЪЄЄЄЮЄЧЁЂКяНќЅъЅЙЅШЄђЛШЄІЪ§МАЄЫНЄРЕЄЙЄыЩЌЭзЄЌЄЂЄъЄоЄЙЁЃ
IE10ЄЧЄтЁЂUint8ClampedArrayЁЪЫАЯТБщЛЛЩеЄ8bitЁЫЄЫЄЯТаБўЄЗЄЦЄЄЄЪЄЄЄЮЄЧЁЂ
ЄГЄЮЅЕЅѓЅзЅыЄЧЄЯЁЂUint8ArrayЄђЛШЄУЄЦЄЄЄоЄЙЁЃ
(Chrome,FFЄЧЄЮЁЂImageData.dataЄЮЗПЄЯUint8ClampedArrayЄЧЄЙЁЃ)
ЄГЄЮЅыЁМЅзПєЄЫЄЪЄыЄШChromeЄфFFЄЯТЎЄЄЄЧЄЙЄЌЁЂIEЄРЄШЄЋЄЪЄъУйЄЄЄЮЄЧЁЂ
ВшСќЅЕЅЄЅКЄЫЄшЄУЄЦЄЯЁЂWeb WorkersЄЫЄшЄыЅоЅыЅСЅЙЅьЅУЅЩВНЄђИЁЦЄЄЙЄыЩЌЭзЄЌЄЂЄъЄоЄЙЁЃ
УЂЄЗЁЂIEЄЧЄЯImageData.dataЄЮЗП(CanvasPixelArray)ЄЌАлЄЪЄыЄЮЄЧЁЂУэАеЄЌЩЌЭзЄЧЄЙЁЃ
--------------- ЪИИЅ ---------------
ЁкХФТМЄЮЪ§МАЁл
H. Tamura: A comparison of line thinning algorithms from digital geometry viewpoint, Proc. 4th Int. Joint Conf. on Pattern Recognition, pp. 715 - 719 (1978.11)
ЁкZhang-SuenЄЮЪ§МАЁл
Zhang, T. Y. and Suen, Ching Y., ЁШA Fast Parallel Algorithms ForThinning Digital PatternsЁЩ,Communication of the ACM,Vol 27, No. 3,Maret 1984, pp.236-239.
ЁкNWGЄЮЪ§МАЁл
P.S.P. Wang and Y.Y. Zhang (1989). A fast and flexible thinning algo-rithm. IEEE Transactions on Computation C-38, 741–745
Tags: ЅзЅэЅАЅщЅрЅсЅт
ЅыЁМЅзВѓПєЄЌЄЩЄІЄЗЄЦЄтТПЄЏЄЪЄыЄЮЄЧЁЂjavascriptЄЧЄЮМТСѕЮуЄЯОЏЄЪЄЄЄЧЄЙЁЃ
ЄГЄГЄЧЄЯЁЂШцГгХЊЙтТЎЄЪZhang-Suen, NWGЄШЁЂХФТМЄЮЪ§МАЄђМТСѕЄЗЄЦЄпЄоЄЙЁЃ
МТЙдЅЕЅѓЅзЅыЄЯЄГЄСЄщ
Zhang-SuenЄЮЅЂЅыЅДЅъЅКЅрЄЯЁЂШцГгХЊУБНуЄЧЄЂЄыЄЮЄЧМТСѕЄЗАзЄЄЄЧЄЙЁЃ
ЅщЅЙЅПЅЙЅЅуЅѓЄЫЄшЄъВшСЧО№ЪѓЄђЦЩЄпЙўЄпЁЂ
ФДККВшСЧЄђДоЄрЁЂ3x3pixЄЮВшСЧУЭЄЫТаЄЗЁЂ3МяЄЮОђЗяЄђЫўЄПЄЗЄЦЄЄЄьЄаЁЂ
ФДККВшСЧЄђЧђ(1)ЄЋЄщЙѕ(0)ЄЫУжЄДЙЄЈЄоЄЙЁЃ
ФДККВшСЧ(P1)ЄђДоЄрЁЂ3x3pixЄЮВшСЧЄЫМЁЄЮЄшЄІЄЫШжЙцЄђПЖЄыЁЃ

ОђЗяЃБЁЅ
ЁЁГАМўАьМўЄђФЏЄсЄПЛўЁЂ
ЁЁ(P2->P3->P4->P5->P6->P7->P8->P9->P2)
ЁЁЙѕЂЊЧђЄШЄЪЄыЪТЄгЄЌАьЄФЄРЄБЄЧЄЂЄыЄГЄШЁЃ
ЁЁ(БбЪИ:A(P1)=number of 0,1 patterns(transitions from 0 to 1) in the ordered sequence of P2,P3,P4,P5,P6,P7,P8,P9,P2.
ЁЁCondition: A(P1) = 1 )
ОђЗяЃВЁЅ
ЁЁГАМўЄЮВУЛЛ(ЧђЄЪЄщ+1)ЄЮЗыВЬ(B)ЄЌЁЂ2<= B <=6ЁЂЄђЫўЄПЄЙЁЃ
ЁЁ(БбЪИ:B(P1)=P2+P3+P4+P5+P6+P7+P8+P9 (number of nonzero neighbords of P1.)
ЁЁCondition: 2 <= B(P1) <= 6 )
ОђЗяЃГ(1)ЁЅ
ЁЁP2 x P4 x P6 = 0 ЄЋЄФЁЂP4 x P6 x P8 = 0 ЄђЫўЄПЄЙЁЃ
ОђЗяЃГ(2)ЁЅ
ЁЁP2 x P4 x P8 = 0 ЄЋЄФЁЂP2 x P6 x P8 = 0 ЄђЫўЄПЄЙЁЃ
ЄоЄКЁЂОђЗяЃБЁЅЃВЁЅЃГ(1)ЄЮШНФъЄђЙдЄЄЁЂОђЗяЄђЫўЄПЄЗЄПОьЙчЁЂГКХіВшСЧЄђНќЕюЅъЅЙЅШЄЫФЩВУЄЙЄыЁЃ
СДВшСЧФДККИхЁЂНќЕюЅъЅЙЅШЄЫВшСЧЄЌЄЂЄьЄаЁЂЄНЄЮВшСЧЄђСДЄЦЙѕ(0)ЄЫЪбЄЈЄыЁЃЄЪЄБЄьЄаНЊЮЛЄЙЄыЁЃ
МЁЄЫЁЂОђЗяЃБЁЅЃВЁЅЃГ(2)ЄЮШНФъЄђЙдЄЄЁЂЦБЭЭЄЮНшЭ§ЄђТГЄБЄыЁЃ
АЪЙпЁЂОђЗяЃГ(1)(2)ЄђРкЄъТиЄЈЄЪЄЌЄщЁЂОђЗяЄђЫўЄПЄЙВшСЧЄЌЄЪЄЏЄЪЄыЄоЄЧЁЂЗЋЄъЪжЄЗЙдЄІЁЃ
NWG (Nagendraprasad-Wang-Gupta)ЄЫЄФЄЄЄЦ ЄЯЁЂZhang-SuenЄШШѓОяЄЫЛїЄПНшЭ§ЄЧЄЂЄыЄПЄсЁЂ
РтЬРЄЯГфАІЄЗЄоЄЙЁЃ
ОмКйЄЯЁЂЅНЁМЅЙЅГЁМЅЩЄЋЁЂ
A note on the Nagendraprasad-Wang-Gupta thinning algorithm ЄђЄДЭїЄЏЄРЄЕЄЄЁЃ
Zhang-SuenЄЮЅЂЅыЅДЅъЅКЅрЄЌМчЄЫЗзЛЛЄЫЄшЄыШНФъЄђЙдЄІЄЮЄЫТаЄЗЁЂ
ХФТМЄЮЅЂЅыЅДЅъЅКЅрЄЯЁЂПоЗСЄЮЅоЅУЅСЅѓЅАЄђЭјЭбЄЗЄоЄЙЁЃ
ТчЄоЄЋЄЪНшЭ§ЄШЄЗЄЦЄЯЁЂ
2МяЮрЄЮЅбЅПЁМЅѓЄЌЄЂЄъЁЂЄНЄьЄОЄьЄЮЅбЅПЁМЅѓЄЯЁЂ
3x3ЄЮНќЕюЅбЅПЁМЅѓЄШ3x3ЄЮШѓНќЕюЅбЅПЁМЅѓЄЫЪЌЄЋЄьЄыЁЃ
ЁЪЄГЄГЄЧИРЄІНќЕюЄЯЁЂЧђЄЋЄщЙѕЄиЄЮЪбЙЙЄђАеЬЃЄЙЄыЁЃЁЫ
ЅщЅЙЅПЅЙЅЅуЅѓЄЫЄшЄъВшСЧО№ЪѓЄђЦЩЄпЙўЄпЁЂ
ГЦВшСЧЄЫЄФЄЄЄЦ3x3ЄЮЅбЅПЁМЅѓЅоЅУЅСЅѓЅАЄђЙдЄІЁЃ
ЅбЅПЁМЅѓЄЫЄЯМЁЄЮЄтЄЮЄЌЄЂЄыЁЃ

ЁкНшЭ§ГЕЭзЁл
Ё ЅбЅПЁМЅѓЃБЄЮНќЕюЅбЅПЁМЅѓЄЧЅоЅУЅСЅѓЅАЄЙЄьЄаЂЄиЁЂАьУзЄЗЄЪЄБЄьЄаМЁВшСЧЄиЁЃ
Ђ ЅбЅПЁМЅѓЃБЄЮШѓНќЕюЅбЅПЁМЅѓЄЧЅоЅУЅСЅѓЅАЄЙЄьЄаМЁВшСЧЄиЁЂАьУзЄЗЄЪЄБЄьЄаЃЄиЁЃ
Ѓ ГКХіВшСЧЄђНќЕюЅъЅЙЅШЄЫФЩВУЄЗЁЂМЁВшСЧЄиЁЃ
Є ЁЁСЃЄЮНшЭ§ЄђСДВшСЧЄЫТаЄЗЄЦЙдЄІЁЃ
Ѕ НќЕюЅъЅЙЅШЄЫВшСЧЄЌЄЂЄьЄаЁЂЄНЄЮВшСЧЄђСДЄЦЙѕ(0)ЄЫЪбЄЈЄыЁЃЄЪЄБЄьЄаНЊЮЛЁЃ
І ЅбЅПЁМЅѓЃВЄЮНќЕюЅбЅПЁМЅѓЄЧЅоЅУЅСЅѓЅАЄЙЄьЄаЇЄиЁЂАьУзЄЗЄЪЄБЄьЄаМЁВшСЧЄиЁЃ
Ї ЅбЅПЁМЅѓЃВЄЮШѓНќЕюЅбЅПЁМЅѓЄЧЅоЅУЅСЅѓЅАЄЙЄьЄаМЁВшСЧЄиЁЂАьУзЄЗЄЪЄБЄьЄаЈЄиЁЃ
Ј ГКХіВшСЧЄђНќЕюЅъЅЙЅШЄЫФЩВУЄЗЁЂМЁВшСЧЄиЁЃ
Љ ІЁСЈЄЮНшЭ§ЄђСДВшСЧЄЫТаЄЗЄЦЙдЄІЁЃ
Њ НќЕюЅъЅЙЅШЄЫВшСЧЄЌЄЂЄьЄаЁЂЄНЄЮВшСЧЄђСДЄЦЙѕ(0)ЄЫЪбЄЈЄыЁЃЄЪЄБЄьЄаНЊЮЛЁЃ
Ћ ЁЄЫЬсЄыЁЃ
ЁкЅоЅУЅСЅѓЅАЅГЁМЅЩЮуЁл
РтЬРЄЮАйЄЫЁЂ3x3pixЄЧЩНИНЄЕЄьЄыЃБЄФЄЮЅбЅПЁМЅѓЄЫP0ЁСP8ЄЮШжЙцЄђПЖЄъЄоЄЙЁЃ

P0ЁСP8ЄђГЦ2bitЄЧЩНЄЙЄтЄЮЄШЄЗЁЂ
Чђbit:10, Йѕbit:01, ЄЩЄСЄщЄЧЄтЮЩЄЄЄтЄЮЄЯbit:00ЁЁЄШЄЗЄоЄЙЁЃ
ГЦЮѓЄЮРшЦЌ2bitЄЫ00ЄђЩеВУЄЗЁЂЃБЅаЅЄЅШ/ЮѓЄЧЩНИНЄЙЄыЄШЁЂ
ЃБЅбЅПЁМЅѓЄЯЃГЅаЅЄЅШЄЫЄЪЄъЄоЄЙЁЃ
ЮуЄЈЄаЁЂЅбЅПЁМЅѓЃБЄЮНќЕюЅбЅПЁМЅѓЄЧЄЂЄьЄаЁЂ

ЄГЄГЄЧЁЂЄЂЄыВшСЧЄђДоЄр3x3pixЄЮОѕТжЄЌМЁЄЮЭЭЄЫЄЪЄУЄЦЄЄЄыЄШЄЙЄыЄШ

ЄГЄьЄЯЁЂЅбЅПЁМЅѓЃБЁІШѓНќЕюЅбЅПЁМЅѓЄЮ6ШжЬмЄШЅоЅУЅСЄЗЄоЄЙЁЃ

ШѓНќЕюЅбЅПЁМЅѓ(6)ЄЯЁЂP = 0x040A04ЄЧЩНИНЄЕЄьЄыЄЮЄЧ
G AND P = P ЄЌРЎЄъЮЉЄФЁЃ
ЄГЄЮЯРЭ§МАЄЌРЎЄъЮЉЄФОьЙчЄЫЁЂЅбЅПЁМЅѓЅоЅУЅСЄШЧЇФъЄЧЄЄоЄЙЁЃ
ХФТМЄЮЪ§МАЄЧЄЯЁЂЄНЄьЄлЄЩЅбЅПЁМЅѓЄЌТПЄЏЄЪЄЄЄЮЄЧЁЂ
ГфЄШДЪУБЄЪЅГЁМЅЧЅЃЅѓЅАЄЧКбЄпЄоЄЙЁЃ
<!DOCTYPE html> <html> <!-- // (c)Hundredsoft Corporation. 2013 All right reserved. // // UTF-8ЄЧЪнТИЄЗЄЦВМЄЕЄЄ --> <head> <meta http-equiv="Content-Type" content="text/html; charset=utf-8" /> <meta http-equiv="X-UA-Compatible" content="IE=edge" /> <meta name="viewport" content="width=device-width, initial-scale=1.0, user-scalable=no" /> <title>КйРўВНЅЕЅѓЅзЅы</title> <script type="text/javascript"> // // Zhang-Suen Algorithm // var zhangsuen = function(imgdata){ var w = imgdata.width; var h = imgdata.height; var ind = imgdata.data; var x, y, rAry; var bFlag = true; for (var k=0; k<100 && bFlag; k++){ if (!(k & 1)){ bFlag = false; } rAry = new Uint8Array(ind); for (y=1; y<h-1; y++){ for (x=1; x<w-1; x++){ var i = (y*w + x)*4; if (rAry[i]){ var a,b,p1,p2,p3,p4,p5,p6,p7,p8,p9; // [p9 p2 p3] // [p8 p1 p4] // [p7 p6 p5] p1 = 1; p2 = (rAry[i-w*4 ]) ? 1 : 0; p3 = (rAry[i-w*4+4]) ? 1 : 0; p4 = (rAry[i +4]) ? 1 : 0; p5 = (rAry[i+w*4+4]) ? 1 : 0; p6 = (rAry[i+w*4 ]) ? 1 : 0; p7 = (rAry[i+w*4-4]) ? 1 : 0; p8 = (rAry[i -4]) ? 1 : 0; p9 = (rAry[i-w*4-4]) ? 1 : 0; a = 0; if (!p2 && p3){a++;} if (!p3 && p4){a++;} if (!p4 && p5){a++;} if (!p5 && p6){a++;} if (!p6 && p7){a++;} if (!p7 && p8){a++;} if (!p8 && p9){a++;} if (!p9 && p2){a++;} b = p2+p3+p4+p5+p6+p7+p8+p9; if (a == 1 && 2 <= b && b <= 6){ if ((!(k & 1) && p2*p4*p6 == 0 && p4*p6*p8 == 0) || ( (k & 1) && p2*p4*p8 == 0 && p2*p6*p8 == 0)) { ind[i] = ind[i+1] = ind[i+2] = 0; bFlag = true; } } } } } } }; // // NWG Algorithm // var nwg_method = function(imgdata){ var w = imgdata.width; var h = imgdata.height; var ind = imgdata.data; var x, y, rAry; var bFlag = true; for (var k=0; k<100 && bFlag; k++){ bFlag = false; rAry = new Uint8Array(ind); for (y=1; y<h-1; y++){ for (x=1; x<w-1; x++){ var i = (y*w + x)*4; if (rAry[i]){ var a,b,c,e,f,p0,p1,p2,p3,p4,p5,p6,p7; // [p7 p0 p1] // [p6 p2] // [p5 p4 p3] p0 = (rAry[i-w*4 ]) ? 1 : 0; p1 = (rAry[i-w*4+4]) ? 1 : 0; p2 = (rAry[i +4]) ? 1 : 0; p3 = (rAry[i+w*4+4]) ? 1 : 0; p4 = (rAry[i+w*4 ]) ? 1 : 0; p5 = (rAry[i+w*4-4]) ? 1 : 0; p6 = (rAry[i -4]) ? 1 : 0; p7 = (rAry[i-w*4-4]) ? 1 : 0; a = 0; if (!p0 && p1){a++;} if (!p1 && p2){a++;} if (!p2 && p3){a++;} if (!p3 && p4){a++;} if (!p4 && p5){a++;} if (!p5 && p6){a++;} if (!p6 && p7){a++;} if (!p7 && p0){a++;} b = p0+p1+p2+p3+p4+p5+p6+p7; if (2 <= b && b <= 6){ c = 0; if ((p0+p1+p2+p5 == 0 && p4+p6 == 2) || (p2+p3+p4+p7 == 0 && p0+p6 == 2)){ c = 1; } if (a == 1 || c == 1){ e = (p2+p4) * p0 * p6; f = (p0+p6) * p2 * p4; if ((!(k & 1) && e == 0) || ( (k & 1) && f == 0)){ ind[i] = ind[i+1] = ind[i+2] = 0; bFlag = true; } } } } } } } }; // // ХФТМ Algorithm // var tamura = function(imgdata){ // [p0 p1 p2] // [p3 p4 p5] // [p6 p7 p8] // // P[0-8]Єђ2bitЄЧЩНЄЙЁЃЧђbit:10, Йѕbit:01, ЄНЄЮТОbit:00 // РшЦЌЄЫbit00ЄђЩеВУЄЗЁЂЃБЅаЅЄЅШ/ЮѓЄЧЃБЄФЄЮЅбЅПЁМЅѓЄђЃГЅаЅЄЅШЄЧЩНИНЁЃ // BitЪТЄгЄЯЁЂ00[p0][p1][p2]00[p3][p4][p5]00[p6][p7][p8]ЄШЄЙЄыЁЃ // НќЕюЄЙЄыЅбЅПЁМЅѓ(1) var pat1 = new Array(0x040800, 0x000900); // НќЕюЄЗЄЪЄЄЅбЅПЁМЅѓ(1) var pat1n = new Array(0x040a09, 0x182900, 0x001908, 0x042804, 0x081900, 0x040a04, 0x001824, 0x241800, 0x060900, 0x000906, 0x192a11, 0x190a19, 0x112a19, 0x192819); // НќЕюЄЙЄыЅбЅПЁМЅѓ(2) var pat2 = new Array(0x000804, 0x001800); // НќЕюЄЗЄЪЄЄЅбЅПЁМЅѓ(2) var pat2n = new Array(0x182804, 0x001a09, 0x001908, 0x042804, 0x081900, 0x040a04, 0x001824, 0x241800, 0x060900, 0x000906, 0x192a11, 0x190a19, 0x112a19, 0x192819); var w = imgdata.width; var h = imgdata.height; var ind = imgdata.data; var bFlag = true; for (var k=0; k<100 && bFlag; k++){ bFlag = false; var rAry = new Uint8Array(ind); var pat, patn; if (k & 1){ pat = pat2; patn = pat2n; }else{ pat = pat1; patn = pat1n; } var x,y; for (y=1; y<h-1; y++){ for (x=1; x<w-1; x++){ var i = (y*w + x)*4; if (rAry[i]){ var f = 0x000800; if (rAry[i-w*4-4]){f |= 0x200000;} else {f |= 0x100000;} if (rAry[i-w*4 ]){f |= 0x080000;} else {f |= 0x040000;} if (rAry[i-w*4+4]){f |= 0x020000;} else {f |= 0x010000;} if (rAry[i -4]){f |= 0x002000;} else {f |= 0x001000;} // if (rAry[i ]){f |= 0x000800;} // else {f |= 0x000400;} if (rAry[i +4]){f |= 0x000200;} else {f |= 0x000100;} if (rAry[i+w*4-4]){f |= 0x000020;} else {f |= 0x000010;} if (rAry[i+w*4 ]){f |= 0x000008;} else {f |= 0x000004;} if (rAry[i+w*4+4]){f |= 0x000002;} else {f |= 0x000001;} // НќЕюЄЙЄыЅбЅПЁМЅѓЄЫАьУз if ((f & pat[0]) == pat[0] || (f & pat[1]) == pat[1]){ // НќЕюЄЗЄЪЄЄЅбЅПЁМЅѓЄЫАьУз if ((f & patn[ 0]) == patn[ 0] || (f & patn[ 1]) == patn[ 1] || (f & patn[ 2]) == patn[ 2] || (f & patn[ 3]) == patn[ 3] || (f & patn[ 4]) == patn[ 4] || (f & patn[ 5]) == patn[ 5] || (f & patn[ 6]) == patn[ 6] || (f & patn[ 7]) == patn[ 7] || (f & patn[ 8]) == patn[ 8] || (f & patn[ 9]) == patn[ 9] || (f & patn[10]) == patn[10] || (f & patn[11]) == patn[11] || (f & patn[12]) == patn[12] || (f & patn[13]) == patn[13]){ ; }else{ ind[i] = ind[i+1] = ind[i+2] = 0; bFlag = true; } } } } } } }; var thinning = function(pattern){ var chk = document.getElementById('difftm') var cvs = document.getElementById('IDcanvas') var ctx = cvs.getContext("2d"); var imgdata = ctx.getImageData(0, 0, cvs.width, cvs.height); var stt = new Date; if (pattern == 0){ tamura(imgdata); }else if (pattern == 1){ zhangsuen(imgdata); }else{ nwg_method(imgdata); } chk.innerHTML = "ConvertTime:" + ((new Date) - stt) + "ms"; ctx.putImageData(imgdata, 0, 0); }; var init = function(filename){ var cvs = document.getElementById('IDcanvas') var ctx = cvs.getContext("2d"); var img = new Image(); img.onload = (function(){ ctx.drawImage(img, 0, 0); }); img.src = filename; }; </script> </head> <body onload="init('test.png');"> <canvas id="IDcanvas" width="512" height="512"></canvas> <hr /> <input type="button" value="ВшСќЃБ" style="width:100px; height:50px;" onclick="init('test.png'); return false;"> <input type="button" value="ВшСќЃВ" style="width:100px; height:50px;" onclick="init('test2.png'); return false;"> <input type="button" value="ВшСќЃГ" style="width:100px; height:50px;" onclick="init('test3.png'); return false;"> <br /> <input type="button" value="ХФТМ" style="width:100px; height:50px;" onclick="thinning('0'); return false;"> <input type="button" value="Zhang-Suen" style="width:100px; height:50px;" onclick="thinning('1'); return false;"> <input type="button" value="NWG" style="width:100px; height:50px;" onclick="thinning('2'); return false;"> <hr /> ВшСќЄђСЊЄѓЄЧЄЋЄщЁЂХФТМ or Zhang-Suen oe NWG ЄђЅЏЅъЅУЅЏЁЊ<br /> ЁЪChrome,FireFoxЄРЄШ0.5ЩУФјХйЄЧЄЙЄЌЁЂIE10ЄРЄШЪбДЙЄЫ5ЩУФјХйГнЄъЄоЄЙЁЃЁЫ<br /> <br /> <div id="difftm"></div> </body> </html>
РтЬРЄЧЄЯКяНќЅъЅЙЅШЄђЛШЄУЄЦЄЄЄоЄЙЄЌЁЂИЕЅЧЁМЅПЄђTypedArray(Uint8Array)ЄЫЅГЅдЁМЄЗЄПЪ§ЄЌСсЄЋЄУЄПЄЮЄЧЁЂ
МТСѕЄЧЄЯЁЂЪбЄЈЄЦЄЄЄоЄЙЁЃ(ЦтЭЦХЊЄЫЪбЄяЄыЄтЄЮЄЧЄЯЄЂЄъЄоЄЛЄѓЁЃ)
Zhang-Suen,NWG,ХФТМЄЧЁЂЄЩЄЮЪ§ЫЁЄЌЮЩЄЄЄЋЄЯЁЂЦўЮЯВшСќЄЫЄшЄУЄЦЪбЄяЄыЄЮЄЧАьГЕЄЫЄЯИРЄЈЄоЄЛЄѓЁЃ
ЅЕЅѓЅзЅыЄђЦАЄЋЄЙЄШЄяЄЋЄъЄоЄЙЄЌЁЂНшЭ§ЛўДжЄЫДиЄЗЄЦЄЯЁЂNWGЄшЄъЁЂZhang-SuenЄЮЪ§ЄЌСсЄЄЄЧЄЙЁЃ
NWGЄЯЁЂZhang-SuenЄЮВўЮЩШЧЄЧЄЂЄыЄПЄсМуДГНшЭ§ЄЌС§ЄЈЄЦЄЄЄыЄПЄсЄЧЄЙЁЃ
ПЭДжЄЮЬмЄЧИЋЄыЄШЖЯЄЋЄЪАуЄЄЄЧЄЙЄЌЁЂNWGЄЮЪ§ЄЌхКЮяЄЫЄЪЄУЄЦЄЄЄыЄшЄІЄЧЄЙЁЃ
ХФТМЄЫДиЄЗЄЦЄЯЁЂЅЕЅѓЅзЅыЄЮВшСќЃБЁІВшСќЃВЄЧЄЯТЎХйЄЌЮєЄъЄоЄЙЄЌЁЂВшСќЃГЄЧЄЯАЕХнХЊЄЫСсЄЄЄЧЄЙЁЃ
ЪИЛњЗЯЄЧЄЯЬЏЄЪЄвЄВЄЌНаЄфЄЙЄЄЄЧЄЙЄЌЁЂМЬППХљЄЮЅЈЅУЅИУъНаВшСќЄЫТаЄЗЄЦЄЯЮЩЄЄЗыВЬЄЌНаЄЦЄЄЄоЄЙЁЃ
(ЯРЪИШЏЩННчЄЧЄЯЁЂЁкHilditch(1968)ЁлЂЊЁкХФТМ(1978)ЁлЂЊЁкZhang-Suen(1984)ЁлЂЊЁкNWG(1989)Ёл)
КЃВѓМТСѕЄЗЄЦЄЄЄоЄЛЄѓЄЌЁЂ
HilditchЄЮЪ§ЫЁЄЯКйРўВННшЭ§ЄЮИЕСФЄШЄтИРЄЈЄоЄЙЄЌЁЂННЪЌЄЪЗыВЬЄЌЦРЄщЄьЄЪЄЄОьЙчЄЌЄЂЄыЄщЄЗЄЄЁЃ
RosenfeldЄЯЁЂZhang-Suen,NWG,ХФТМЄЫШцЄйЁЂЄЋЄЪЄъНшЭ§ЄЌНХЄЏЄЪЄыЄщЄЗЄЄЁЃ
ЁЪЛВЙЭЁЇ Comparing Hilditch, Rosenfeld, Zhang-Suen,and Nagendraprasad - Wang-Gupta Thinning ЁЫ
МТЙдЅЕЅѓЅзЅыЄЯЄГЄСЄщ
IE10/Chrome/FF/AndroidЄЧЁЂГЮЧЇЄЗЄЦЄЄЄоЄЙЁЃ
IE9ЄЯЁЂTypedArray(Uint8Array)ЄЫТаБўЄЗЄЦЄЄЄЪЄЄЄЮЄЧЁЂКяНќЅъЅЙЅШЄђЛШЄІЪ§МАЄЫНЄРЕЄЙЄыЩЌЭзЄЌЄЂЄъЄоЄЙЁЃ
IE10ЄЧЄтЁЂUint8ClampedArrayЁЪЫАЯТБщЛЛЩеЄ8bitЁЫЄЫЄЯТаБўЄЗЄЦЄЄЄЪЄЄЄЮЄЧЁЂ
ЄГЄЮЅЕЅѓЅзЅыЄЧЄЯЁЂUint8ArrayЄђЛШЄУЄЦЄЄЄоЄЙЁЃ
(Chrome,FFЄЧЄЮЁЂImageData.dataЄЮЗПЄЯUint8ClampedArrayЄЧЄЙЁЃ)
ЄГЄЮЅыЁМЅзПєЄЫЄЪЄыЄШChromeЄфFFЄЯТЎЄЄЄЧЄЙЄЌЁЂIEЄРЄШЄЋЄЪЄъУйЄЄЄЮЄЧЁЂ
ВшСќЅЕЅЄЅКЄЫЄшЄУЄЦЄЯЁЂWeb WorkersЄЫЄшЄыЅоЅыЅСЅЙЅьЅУЅЩВНЄђИЁЦЄЄЙЄыЩЌЭзЄЌЄЂЄъЄоЄЙЁЃ
УЂЄЗЁЂIEЄЧЄЯImageData.dataЄЮЗП(CanvasPixelArray)ЄЌАлЄЪЄыЄЮЄЧЁЂУэАеЄЌЩЌЭзЄЧЄЙЁЃ
--------------- ЪИИЅ ---------------
ЁкХФТМЄЮЪ§МАЁл
H. Tamura: A comparison of line thinning algorithms from digital geometry viewpoint, Proc. 4th Int. Joint Conf. on Pattern Recognition, pp. 715 - 719 (1978.11)
ЁкZhang-SuenЄЮЪ§МАЁл
Zhang, T. Y. and Suen, Ching Y., ЁШA Fast Parallel Algorithms ForThinning Digital PatternsЁЩ,Communication of the ACM,Vol 27, No. 3,Maret 1984, pp.236-239.
ЁкNWGЄЮЪ§МАЁл
P.S.P. Wang and Y.Y. Zhang (1989). A fast and flexible thinning algo-rithm. IEEE Transactions on Computation C-38, 741–745
Tags: ЅзЅэЅАЅщЅрЅсЅт
author : HUNDREDSOFT | - | -