x64でも拡張倍精度を使いたい
| プログラムメモ | 2012/05/13 Sun 00:04
x64では最低でもSSE2まで使えるので、今更FPUを使うことはあまりありません。
もし、倍精度(仮数部53bit)でも精度が足りない場合、
SSE2を使って4倍精度浮動小数点ライブラリを組むか、
4倍精度に対応した x64向けのコンパイラを用意するのが普通でしょう。
しかし、計算速度を要求されるようなケースで、もし64bit精度で足りるなら、
FPUによる拡張倍精度(仮数部64bit)という選択肢もあります。
(例えば10進で、あと1桁だけ精度が欲しい場合にコンパイラまで変えないですよね)
以前にx86用の拡張倍精度クラスを書きましたが、
今度はx64用のサンプルコード。
x64では、インラインアセンブラが使えないので、組み込み関数(Compiler Intrinsics)を使うか、
MASM ( ml64.exe ) を使ってアセンブリをコーディングするかの選択になりますが、
FPUを使うので、ml64用の.asmファイルを作ることにします。
ターゲットは、x64 のWindowsで Visual Studio で開発しているものとします。
他のコンパイラだと呼び出し規約( MSのFastCall )が異なることがあるので注意。
double をオーバーラップするような Ldouble クラスを作る事にします。
メンバとして、拡張倍精度のデータを1つ持ちます。
必要なのは 10バイトですが、切りの良いところで 16バイト取っています。
まず、ヘッダーファイル「Ldouble.h」です。
基本的な演算をクラスに入れて、三角関数,指数関数等を外部関数として呼び出せるようにしています。
アセンブリで作成するのは、extern "C"の関数群です。
これが「Ldouble.asm」です。
最後に、Ldoubleクラスを使ったサンプルコード「main.cpp」です。
VS2010でBuildする際は、新規プロジェクト(VisualC++,Win32,Win32コンソールアプリケーション,空のプロジェクト)で、
ソース( Ldouble.asm, Ldouble.h, main.cpp )を追加して、
構成マネージャーでプラットフォームをx64にします。
新規でx64が選べない場合は、VC++2010の64bit対応のインストールが足りないかもしれません。
その場合は、ml64.exeも入ってないかもしれないので確認して下さい。
続いて、ソリューションエクスプローラの Ldouble.asm を右クリックして、プロパティ。
構成プロパティ・全般で項目の種類→カスタムビルドツールに変更して下さい。
全般の下に出てくるカスタムビルドツールのコマンドライン欄に、
ml64.exe /DWIN_X64 /Zi /c /Cp /Fl /Fo$(IntDir)\$(InputName).obj Ldouble.asm
出力ファイル欄に
$(IntDir)\$(InputName).obj
を指定して下さい。
これで Build が通るようになります。
例外は考えていません。ご利用の際にはFPU制御ワードを適宜設定して下さい。
(Ldouble.asmのdeffcwを変えて下さい。)
Ldoubleへの入力は、double か整数です。
出力は double型 だけです。これは、double へのキャストとして実現されます。
もちろん、LdoubleからLdoubleへのコピーで精度が落ちることはありません。
Ldoubleは、64bit精度を保持していますので、
Ldoubleを使った演算中は常に64bit精度を保ちます。
出力(キャスト) は double(53bit) 精度に丸めた値を返しますが、
Ldouble が持っている値が 53bit に丸められるわけではありません。
この方法はとてもうまく問題を解決してくれるかもしれません。
計算精度ボトムの一部だけをLdoubleによる高精度計算に置き換えて、
その後キャストするだけで、今までの計算ルーチンに戻せます。
例えば、1つの double型のスタック変数を Ldouble にしただけ(1文字修正)で問題が解決するかもしれません。
とても自然に組み込めるのは良いのですが、コードを一見しただけだと変化(影響)がわかりにくいので、
コメントは丁寧に書く必要があります。
さて、Build後にできたexeを実行すると次の結果が得られました。
最後のLeibniz's piを除いては、基本演算の確認です。
左側がdouble演算による結果で、右側がLdouble(FPU)による結果です。
Leibniz's piはライプニッツの公式によるπの計算ですが、
わざと演算量を増やして、処理時間を比較しています。
5,000,000項で打ち切って、演算結果と演算に要した時間を表示します。
演算時間に関しては、double演算のおよそ倍の時間が掛っていますが、
double演算では累積誤差により 14 桁の精度しかありませんが、FPUでは 16 桁の精度があります。
三角関数などを使うと、FPUの方が10倍くらい処理時間が掛ることもあります。
doubleに比べて、11 bit多くの精度を出すため処理時間が掛かるようです。
しかし除算については、double演算とFPUで処理時間は同等でした。
逆アセンブラを見てみると、double演算ではSSE2が使われていますが並列化までは行われていません。
うまく並列化(最適化)できれば、double演算はもう少し早くなります。
(Release-Buildではdouble演算側に多少のベクトル化が行われていました。)
正確さと処理時間のトレードオフですので、どちらが良いというものではありません。
目的に即した解決策が見つけられなければ、このような方法もありかと思います。
上記、掲載ソースを圧縮したものをここに置いておきます。
Tags: プログラムメモ
もし、倍精度(仮数部53bit)でも精度が足りない場合、
SSE2を使って4倍精度浮動小数点ライブラリを組むか、
4倍精度に対応した x64向けのコンパイラを用意するのが普通でしょう。
しかし、計算速度を要求されるようなケースで、もし64bit精度で足りるなら、
FPUによる拡張倍精度(仮数部64bit)という選択肢もあります。
(例えば10進で、あと1桁だけ精度が欲しい場合にコンパイラまで変えないですよね)
以前にx86用の拡張倍精度クラスを書きましたが、
今度はx64用のサンプルコード。
x64では、インラインアセンブラが使えないので、組み込み関数(Compiler Intrinsics)を使うか、
MASM ( ml64.exe ) を使ってアセンブリをコーディングするかの選択になりますが、
FPUを使うので、ml64用の.asmファイルを作ることにします。
ターゲットは、x64 のWindowsで Visual Studio で開発しているものとします。
他のコンパイラだと呼び出し規約( MSのFastCall )が異なることがあるので注意。
double をオーバーラップするような Ldouble クラスを作る事にします。
メンバとして、拡張倍精度のデータを1つ持ちます。
必要なのは 10バイトですが、切りの良いところで 16バイト取っています。
まず、ヘッダーファイル「Ldouble.h」です。
基本的な演算をクラスに入れて、三角関数,指数関数等を外部関数として呼び出せるようにしています。
アセンブリで作成するのは、extern "C"の関数群です。
これが「Ldouble.asm」です。
最後に、Ldoubleクラスを使ったサンプルコード「main.cpp」です。
VS2010でBuildする際は、新規プロジェクト(VisualC++,Win32,Win32コンソールアプリケーション,空のプロジェクト)で、
ソース( Ldouble.asm, Ldouble.h, main.cpp )を追加して、
構成マネージャーでプラットフォームをx64にします。
新規でx64が選べない場合は、VC++2010の64bit対応のインストールが足りないかもしれません。
その場合は、ml64.exeも入ってないかもしれないので確認して下さい。
続いて、ソリューションエクスプローラの Ldouble.asm を右クリックして、プロパティ。
構成プロパティ・全般で項目の種類→カスタムビルドツールに変更して下さい。
全般の下に出てくるカスタムビルドツールのコマンドライン欄に、
ml64.exe /DWIN_X64 /Zi /c /Cp /Fl /Fo$(IntDir)\$(InputName).obj Ldouble.asm
出力ファイル欄に
$(IntDir)\$(InputName).obj
を指定して下さい。
これで Build が通るようになります。
例外は考えていません。ご利用の際にはFPU制御ワードを適宜設定して下さい。
(Ldouble.asmのdeffcwを変えて下さい。)
(参考) FPU制御ワードについて MSB F E D C B A 9 8 7 6 5 4 3 2 1 0 +-----------+-----+-----+-----+----------------+ NC 丸め 精度 NC 例外マスク +-----------+-----+-----+-----+----------------+ 例外マスク bit5〜0 0:無効操作例外 1:デノーマル例外 2:零除算例外 3:オーバーフロー例外 4:アンダーフロー例外 5:不正確結果例外 精度 bit9,8 00: 24bit(単精度) 01: reserved 10: 53bit(倍精度) 11: 64bit(拡張倍精度) 丸め bit11,10 00: 最近値(四捨五入に近い) 01: 切り捨て(floor) 10: 切り上げ(ceil) 11: 零方向切り捨て
Ldoubleへの入力は、double か整数です。
出力は double型 だけです。これは、double へのキャストとして実現されます。
もちろん、LdoubleからLdoubleへのコピーで精度が落ちることはありません。
Ldoubleは、64bit精度を保持していますので、
Ldoubleを使った演算中は常に64bit精度を保ちます。
出力(キャスト) は double(53bit) 精度に丸めた値を返しますが、
Ldouble が持っている値が 53bit に丸められるわけではありません。
この方法はとてもうまく問題を解決してくれるかもしれません。
計算精度ボトムの一部だけをLdoubleによる高精度計算に置き換えて、
その後キャストするだけで、今までの計算ルーチンに戻せます。
例えば、1つの double型のスタック変数を Ldouble にしただけ(1文字修正)で問題が解決するかもしれません。
とても自然に組み込めるのは良いのですが、コードを一見しただけだと変化(影響)がわかりにくいので、
コメントは丁寧に書く必要があります。
さて、Build後にできたexeを実行すると次の結果が得られました。
as:= 1.0000000000000000e+001 bs=: 1.2300000000000000e+002 + : 1.3300000000000000e+002: 1.3300000000000000e+002 - : -1.1300000000000000e+002: -1.1300000000000000e+002 abs: 1.1300000000000000e+002: 1.1300000000000000e+002 if : -1.1300000000000000e+002: -1.1300000000000000e+002 * : 1.2300000000000000e+003: 1.2300000000000000e+003 / : 1.2300000000000001e+001: 1.2300000000000001e+001 % : 3.0000000000000000e+000: 3.0000000000000000e+000 pi : 3.1415926535897931e+000: 3.1415926535897931e+000 sin: 4.9999999999999994e-001: 5.0000000000000000e-001 cos: 8.6602540378443871e-001: 8.6602540378443860e-001 sin: 4.9999999999999994e-001: 5.0000000000000000e-001 cos: 8.6602540378443871e-001: 8.6602540378443860e-001 tan: 5.7735026918962573e-001: 5.7735026918962573e-001 ata: 4.8234790710102493e-001: 4.8234790710102499e-001 at2: 9.8279372324732905e-001: 9.8279372324732905e-001 sqr: 1.4142135623730951e+000: 1.4142135623730951e+000 exp: 1.6439050426651380e+005: 1.6439050426651380e+005 ln : 1.2010000000000000e+001: 1.2010000000000000e+001 pow: 3.3234387002712369e+000: 3.3234387002712369e+000 int: 3.0000000000000000e+000: 3.0000000000000000e+000 dec: 3.2343870027123689e-001: 3.2343870027123672e-001 Machin's pi: 3.1415926535897936e+000: 3.1415926535897931e+000 Leibniz's pi(5000000項での真値): 3.1415924535897932384646433832795 Leibniz's pi(5000000) double(3.1415924535897797e+000) time = 0.036[sec] Leibniz's pi(5000000) Ldouble(3.1415924535897930e+000) time = 0.073[sec]
最後のLeibniz's piを除いては、基本演算の確認です。
左側がdouble演算による結果で、右側がLdouble(FPU)による結果です。
Leibniz's piはライプニッツの公式によるπの計算ですが、
わざと演算量を増やして、処理時間を比較しています。
5,000,000項で打ち切って、演算結果と演算に要した時間を表示します。
演算時間に関しては、double演算のおよそ倍の時間が掛っていますが、
double演算では累積誤差により 14 桁の精度しかありませんが、FPUでは 16 桁の精度があります。
三角関数などを使うと、FPUの方が10倍くらい処理時間が掛ることもあります。
doubleに比べて、11 bit多くの精度を出すため処理時間が掛かるようです。
しかし除算については、double演算とFPUで処理時間は同等でした。
逆アセンブラを見てみると、double演算ではSSE2が使われていますが並列化までは行われていません。
うまく並列化(最適化)できれば、double演算はもう少し早くなります。
(Release-Buildではdouble演算側に多少のベクトル化が行われていました。)
正確さと処理時間のトレードオフですので、どちらが良いというものではありません。
目的に即した解決策が見つけられなければ、このような方法もありかと思います。
上記、掲載ソースを圧縮したものをここに置いておきます。
Tags: プログラムメモ
author : HUNDREDSOFT | - | -
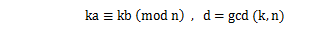 ならば
ならば