�ݥ����GO �����ͷ�
| �ץ�������� | 2017/03/28 Tue 00:18
�ݥ����GO�Ǥϡ�¿���Υȥ졼�ʡ����Ƕ��Υݥ�����õ���Ƥ��ޤ���
��������100%�����ͤȸƤФ��Ƕ��ݥ��������뤳�Ȥϡ���ä��ˤ���ޤ���
�ʤΤǡ�90%��80%�Dz�������櫓�Ǥ��������Ρ��ɽ����������ͤȤϲ��������Ȼפ���Ĵ�٤Ƥߤޤ�����
�ƥݥ����ˤϡ����ܤȤʤ��²�͡ʹ����ϡ��ɸ��ϡ����ϡˤ����ꤵ��Ƥ��ơ�
���줾��θ��Τˤϡ��ܦ��Ȥʤ롢�����ϡ��ɸ��ϡ����Ϥ�Ϳ�����롣
��������̾��ɽ��������ͤϡ�������ɽ��CP�����Ϥ�ɽ��HP������ɽ������Ƥ��롣


������ͭ��(Individual)�ϡ������ϡ��ɸ��ϡ����Ϥ��줾��ˡ�0��15���ϰϤǷ��ꤵ��롣
�ݥ����ˤϡ�1��40�Υ�٥뤬���ꡢ0.5�����ߤǻ��ꤵ��롣
���Υ�٥�ϡ��������뤳�Ȥˤ�äơ�0.5�夲�뤳�Ȥ��Ǥ��롣
�ݥ�����٥�ˤ�ꡢCP�����ͤ���դ���ޤ롣
�ݥ������μ�²�ͤ䡢CP�����ͤˤĤ��Ƥϡ��ͥåȾ�������ξ��ФƤ��롣
CP��HP�η���ˡ���狼�ä��Ȥ����ǡ�
�Ǥϡ���ʬ�λ��äƤ���ݥ����θ����ͤϡ��ɤ�������狼��Τ�������
�ͥåȾ�ˤϡ������ͷ����ʤ��Τ����뤬���ɤ���äƷ����Ƥ���Τ�������
HP����ͤ��Ƥߤ롣
�ݥ�����̾�������²�ͤϤ狼�롣�ֶ�����ɬ�פʺ��פ��餪���褽�Υݥ�����٥뤬�狼�롣
�ʤ�С���٥�γ����ϰ�����Ҥ�ü����HP����Ԥ�����������̤˽ФƤ���HP�ȹ��פ���С����줬����Ȥʤ롣
��������ʣ�������Ф뤳�Ȥ�ͤ�����Τǡ��������������Ȥʤ롣
CP��Ʊ���褦�˷���Ԥ���������HP���ǥ�٥���䤬�ʤ��Ƥ���Τǡ�����ʬ�����ǺѤࡣ
��������̤˽ФƤ���CP�ȹ��פ���С���Ϥꤳ��⡢�������Ȥʤ롣
��������ơ��֥�ˤ���ɽ������С���ޤ����ݥ����θ����ͤ��ܰ¤Ȥʤ롣
�����������ˤ��ɾ�����狼��С�������������ʤ���ळ�Ȥ��Ǥ��롣
�����ޤ����С���ϥץ���������Ȥ���������Ǥ���
�����餯�����Υץ����������ϡ���²�ͥơ��֥�ι������Ȼפ��ޤ���
Niantic�Ҥ��ѹ����������פ��ʤ���Фʤ�ʤ����ȤǤ���
�¹ԥ���ץ�Ϥ�����
Chrome, FF ��ư���ǧ���Ƥ��ޤ���
�ʲ��ϥ����������ɤǤ���index.html�Σ��ܤǤ���
Tags: �ץ��������
��������100%�����ͤȸƤФ��Ƕ��ݥ��������뤳�Ȥϡ���ä��ˤ���ޤ���
�ʤΤǡ�90%��80%�Dz�������櫓�Ǥ��������Ρ��ɽ����������ͤȤϲ��������Ȼפ���Ĵ�٤Ƥߤޤ�����
�ƥݥ����ˤϡ����ܤȤʤ��²�͡ʹ����ϡ��ɸ��ϡ����ϡˤ����ꤵ��Ƥ��ơ�
���줾��θ��Τˤϡ��ܦ��Ȥʤ롢�����ϡ��ɸ��ϡ����Ϥ�Ϳ�����롣
��������̾��ɽ��������ͤϡ�������ɽ��CP�����Ϥ�ɽ��HP������ɽ������Ƥ��롣


������ͭ��(Individual)�ϡ������ϡ��ɸ��ϡ����Ϥ��줾��ˡ�0��15���ϰϤǷ��ꤵ��롣
�ݥ����ˤϡ�1��40�Υ�٥뤬���ꡢ0.5�����ߤǻ��ꤵ��롣
���Υ�٥�ϡ��������뤳�Ȥˤ�äơ�0.5�夲�뤳�Ȥ��Ǥ��롣
�ݥ�����٥�ˤ�ꡢCP�����ͤ���դ���ޤ롣
�ݥ������μ�²�ͤ䡢CP�����ͤˤĤ��Ƥϡ��ͥåȾ�������ξ��ФƤ��롣
CP��HP�η���ˡ���狼�ä��Ȥ����ǡ�
�Ǥϡ���ʬ�λ��äƤ���ݥ����θ����ͤϡ��ɤ�������狼��Τ�������
�ͥåȾ�ˤϡ������ͷ����ʤ��Τ����뤬���ɤ���äƷ����Ƥ���Τ�������
HP����ͤ��Ƥߤ롣
�ݥ�����̾�������²�ͤϤ狼�롣�ֶ�����ɬ�פʺ��פ��餪���褽�Υݥ�����٥뤬�狼�롣
�ʤ�С���٥�γ����ϰ�����Ҥ�ü����HP����Ԥ�����������̤˽ФƤ���HP�ȹ��פ���С����줬����Ȥʤ롣
��������ʣ�������Ф뤳�Ȥ�ͤ�����Τǡ��������������Ȥʤ롣
CP��Ʊ���褦�˷���Ԥ���������HP���ǥ�٥���䤬�ʤ��Ƥ���Τǡ�����ʬ�����ǺѤࡣ
��������̤˽ФƤ���CP�ȹ��פ���С���Ϥꤳ��⡢�������Ȥʤ롣
��������ơ��֥�ˤ���ɽ������С���ޤ����ݥ����θ����ͤ��ܰ¤Ȥʤ롣
�����������ˤ��ɾ�����狼��С�������������ʤ���ळ�Ȥ��Ǥ��롣
�����ޤ����С���ϥץ���������Ȥ���������Ǥ���
�����餯�����Υץ����������ϡ���²�ͥơ��֥�ι������Ȼפ��ޤ���
Niantic�Ҥ��ѹ����������פ��ʤ���Фʤ�ʤ����ȤǤ���
�¹ԥ���ץ�Ϥ�����
Chrome, FF ��ư���ǧ���Ƥ��ޤ���
�ʲ��ϥ����������ɤǤ���index.html�Σ��ܤǤ���
<!DOCTYPE html> <html> <head> <meta charset="utf-8" /> <meta name="viewport" content="width=device-width, initial-scale=1.0, user-scalable=no" /> <title>poke5 �����ͷ��ġ���</title> <style> * { margin:0; padding: 0; } body { padding:5px; background:#ace url(kinkoi.jpg); } #namediv input { width:70px; height:25px; font-size:12px; } input.pk_inp { display:block; margin:2px 10px 2px 0; padding: 2px; } form.hyouka input { margin:2px 2px 2px 20px; padding: 2px; } span.inp_lavel { display:block; width:60px; float:left; clear:both; } select { margin:5px; padding: 2px; } table { margin:5px; padding: 2px; } td { width:100px; text-align:center; } </style> <script type="text/javascript"> var mltbl = [ // �ݥ�����٥�˴ؤ���ơ��֥� // ml: �ݥ�����٥� // perc: ��٥�40���Ф����� // c: CP������ // sand: ������ɬ�פʺ� // candy: ������ɬ�פʰ� {ml:1,perc:1.414724036,c:0.094,sand:0,candy:0}, {ml:1.5,perc:2.923932542,c:0.1351374,sand:200,candy:1}, {ml:2,perc:4.433141061,c:0.1663979,sand:200,candy:1}, {ml:2.5,perc:5.942349554,c:0.1926509,sand:200,candy:1}, {ml:3,perc:7.451557498,c:0.2157325,sand:200,candy:1}, {ml:3.5,perc:8.960765971,c:0.2365727,sand:400,candy:1}, {ml:4,perc:10.4699736,c:0.2557201,sand:400,candy:1}, {ml:4.5,perc:11.97918208,c:0.2735304,sand:400,candy:1}, {ml:5,perc:13.48839026,c:0.2902499,sand:400,candy:1}, {ml:5.5,perc:14.99759871,c:0.3060574,sand:600,candy:1}, {ml:6,perc:16.50680775,c:0.3210876,sand:600,candy:1}, {ml:6.5,perc:18.01601622,c:0.335445,sand:600,candy:1}, {ml:7,perc:19.52522443,c:0.3492127,sand:600,candy:1}, {ml:7.5,perc:21.03443291,c:0.3624578,sand:800,candy:1}, {ml:8,perc:22.54364161,c:0.3752356,sand:800,candy:1}, {ml:8.5,perc:24.05285006,c:0.3875924,sand:800,candy:1}, {ml:9,perc:25.56206057,c:0.3995673,sand:800,candy:1}, {ml:9.5,perc:27.07126902,c:0.4111936,sand:1000,candy:1}, {ml:10,perc:28.58047697,c:0.4225,sand:1000,candy:1}, {ml:10.5,perc:30.00849419,c:0.4335117,sand:1000,candy:1}, {ml:11,perc:31.43650994,c:0.4431076,sand:1000,candy:1}, {ml:11.5,perc:32.86452696,c:0.45306,sand:1300,candy:2}, {ml:12,perc:34.29254396,c:0.4627984,sand:1300,candy:2}, {ml:12.5,perc:35.72056114,c:0.4723361,sand:1300,candy:2}, {ml:13,perc:37.14857675,c:0.481685,sand:1300,candy:2}, {ml:13.5,perc:38.5765939,c:0.4908558,sand:1600,candy:2}, {ml:14,perc:40.00461398,c:0.4998584,sand:1600,candy:2}, {ml:14.5,perc:41.43263118,c:0.5087018,sand:1600,candy:2}, {ml:15,perc:42.86064648,c:0.517394,sand:1600,candy:2}, {ml:15.5,perc:44.28866364,c:0.5259425,sand:1900,candy:2}, {ml:16,perc:45.71668075,c:0.5343543,sand:1900,candy:2}, {ml:16.5,perc:47.14469795,c:0.5426358,sand:1900,candy:2}, {ml:17,perc:48.57271292,c:0.5507927,sand:1900,candy:2}, {ml:17.5,perc:50.00073006,c:0.5588306,sand:2200,candy:2}, {ml:18,perc:51.42875488,c:0.5667545,sand:2200,candy:2}, {ml:18.5,perc:52.85677208,c:0.5745692,sand:2200,candy:2}, {ml:19,perc:54.28478797,c:0.5822789,sand:2200,candy:2}, {ml:19.5,perc:55.71280516,c:0.5898879,sand:2500,candy:2}, {ml:20,perc:57.14082102,c:0.5974,sand:2500,candy:2}, {ml:20.5,perc:58.56883825,c:0.6048188,sand:2500,candy:2}, {ml:21,perc:59.99873261,c:0.6121573,sand:2500,candy:2}, {ml:21.5,perc:61.42674981,c:0.6194041,sand:3000,candy:3}, {ml:22,perc:62.8566514,c:0.6265671,sand:3000,candy:3}, {ml:22.5,perc:64.28466862,c:0.6336492,sand:3000,candy:3}, {ml:23,perc:65.7145723,c:0.640653,sand:3000,candy:3}, {ml:23.5,perc:67.14258943,c:0.647581,sand:3500,candy:3}, {ml:24,perc:68.57248641,c:0.6544356,sand:3500,candy:3}, {ml:24.5,perc:70.00050364,c:0.6612193,sand:3500,candy:3}, {ml:25,perc:71.43040741,c:0.667934,sand:3500,candy:3}, {ml:25.5,perc:72.85842452,c:0.6745819,sand:4000,candy:4}, {ml:26,perc:74.28832607,c:0.6811649,sand:4000,candy:4}, {ml:26.5,perc:75.71634322,c:0.6876849,sand:4000,candy:4}, {ml:27,perc:77.14623491,c:0.6941437,sand:4000,candy:4}, {ml:27.5,perc:78.57425209,c:0.7005429,sand:4500,candy:4}, {ml:28,perc:80.00416311,c:0.7068842,sand:4500,candy:4}, {ml:28.5,perc:81.43218023,c:0.7131691,sand:4500,candy:4}, {ml:29,perc:82.86207287,c:0.7193991,sand:4500,candy:4}, {ml:29.5,perc:84.29009019,c:0.7255756,sand:5000,candy:4}, {ml:30,perc:85.71999464,c:0.7317,sand:5000,candy:4}, {ml:30.5,perc:86.43399483,c:0.734741,sand:5000,candy:4}, {ml:31,perc:87.14799422,c:0.7377695,sand:5000,candy:4}, {ml:31.5,perc:87.86199453,c:0.7407856,sand:6000,candy:6}, {ml:32,perc:88.57599299,c:0.7437894,sand:6000,candy:6}, {ml:32.5,perc:89.28999328,c:0.7467812,sand:6000,candy:6}, {ml:33,perc:90.00399022,c:0.749761,sand:6000,candy:6}, {ml:33.5,perc:90.71799057,c:0.7527291,sand:7000,candy:8}, {ml:34,perc:91.43199898,c:0.7556855,sand:7000,candy:8}, {ml:34.5,perc:92.14599918,c:0.7586304,sand:7000,candy:8}, {ml:35,perc:92.85999484,c:0.7615638,sand:7000,candy:8}, {ml:35.5,perc:93.57399517,c:0.7644861,sand:8000,candy:10}, {ml:36,perc:94.28799738,c:0.7673972,sand:8000,candy:10}, {ml:36.5,perc:95.00199776,c:0.7702973,sand:8000,candy:10}, {ml:37,perc:95.71600203,c:0.7731865,sand:8000,candy:10}, {ml:37.5,perc:96.43000241,c:0.776065,sand:9000,candy:12}, {ml:38,perc:97.14399355,c:0.7789328,sand:9000,candy:12}, {ml:38.5,perc:97.85799386,c:0.7817901,sand:9000,candy:12}, {ml:39,perc:98.57199794,c:0.784637,sand:9000,candy:12}, {ml:39.5,perc:99.2859983,c:0.7874736,sand:10000,candy:15}, {ml:40,perc:100,c:0.7903,sand:10000,candy:15} ]; var pktbl = [ // ��²�ͥơ��֥� // no: �ݥ�����ֹ� // name: ̾�� // maxcp: ����ã�(Lv=40) // atk: ��²�� ���� // def: ��²�� �ɸ� // hp: ��²�� ���� {no:1,name:"�ե�������",maxcp:981,atk:118,def:118,hp:90}, {no:2,name:"�ե�������",maxcp:1552,atk:151,def:151,hp:120}, {no:3,name:"�ե����Х�",maxcp:2568,atk:198,def:198,hp:160}, {no:4,name:"�ҥȥ���",maxcp:831,atk:116,def:96,hp:78}, {no:5,name:"�ꥶ����",maxcp:1484,atk:158,def:129,hp:116}, {no:6,name:"�ꥶ���ɥ�",maxcp:2686,atk:223,def:176,hp:156}, {no:7,name:"���˥���",maxcp:808,atk:94,def:122,hp:88}, {no:8,name:"�����",maxcp:1324,atk:126,def:155,hp:118}, {no:9,name:"����å���",maxcp:2291,atk:171,def:210,hp:158}, {no:10,name:"���㥿�ԡ�",maxcp:393,atk:55,def:62,hp:90}, {no:11,name:"�ȥ��",maxcp:419,atk:45,def:94,hp:100}, {no:12,name:"�Х��ե",maxcp:1701,atk:167,def:151,hp:120}, {no:13,name:"�ӡ��ɥ�",maxcp:397,atk:63,def:55,hp:80}, {no:14,name:"��������",maxcp:392,atk:46,def:86,hp:90}, {no:15,name:"���ԥ���",maxcp:1777,atk:169,def:150,hp:130}, {no:16,name:"�ݥå�",maxcp:580,atk:85,def:76,hp:80}, {no:17,name:"�ԥ����",maxcp:1085,atk:117,def:108,hp:126}, {no:18,name:"�ԥ���å�",maxcp:1994,atk:166,def:157,hp:166}, {no:19,name:"����å�",maxcp:588,atk:103,def:70,hp:60}, {no:20,name:"��å�",maxcp:1549,atk:161,def:144,hp:110}, {no:21,name:"���˥�����",maxcp:673,atk:112,def:61,hp:80}, {no:22,name:"���˥ɥ��",maxcp:1814,atk:182,def:135,hp:130}, {no:23,name:"������",maxcp:778,atk:110,def:102,hp:70}, {no:24,name:"�����ܥå�",maxcp:1737,atk:167,def:158,hp:120}, {no:25,name:"�ԥ����奦",maxcp:787,atk:112,def:101,hp:70}, {no:26,name:"�饤���奦",maxcp:2025,atk:193,def:165,hp:120}, {no:27,name:"�����",maxcp:1194,atk:126,def:145,hp:100}, {no:28,name:"����ɥѥ�",maxcp:2328,atk:182,def:202,hp:150}, {no:29,name:"�˥ɥ���",maxcp:736,atk:86,def:94,hp:110}, {no:30,name:"�˥ɥ��",maxcp:1218,atk:117,def:126,hp:140}, {no:31,name:"�˥ɥ�����",maxcp:2338,atk:180,def:174,hp:180}, {no:32,name:"�˥ɥ���",maxcp:739,atk:105,def:76,hp:92}, {no:33,name:"�˥ɥ��",maxcp:1252,atk:137,def:112,hp:122}, {no:34,name:"�˥ɥ���",maxcp:2386,atk:204,def:157,hp:162}, {no:35,name:"�ԥå�",maxcp:1085,atk:107,def:116,hp:140}, {no:36,name:"�ԥ�����",maxcp:2353,atk:178,def:171,hp:190}, {no:37,name:"������",maxcp:774,atk:96,def:122,hp:76}, {no:38,name:"���奦����",maxcp:2157,atk:169,def:204,hp:146}, {no:39,name:"�ץ��",maxcp:713,atk:80,def:44,hp:230}, {no:40,name:"�ץ����",maxcp:1906,atk:156,def:93,hp:280}, {no:41,name:"���Хå�",maxcp:569,atk:83,def:76,hp:80}, {no:42,name:"����Хå�",maxcp:1830,atk:161,def:153,hp:150}, {no:43,name:"�ʥ��Υ���",maxcp:1069,atk:131,def:116,hp:90}, {no:44,name:"�������ϥ�",maxcp:1512,atk:153,def:139,hp:120}, {no:45,name:"��ե쥷��",maxcp:2367,atk:202,def:170,hp:150}, {no:46,name:"�ѥ饹",maxcp:836,atk:121,def:99,hp:70}, {no:47,name:"�ѥ饻����",maxcp:1657,atk:165,def:146,hp:120}, {no:48,name:"����ѥ�",maxcp:902,atk:100,def:102,hp:120}, {no:49,name:"���ե���",maxcp:1937,atk:179,def:150,hp:140}, {no:50,name:"�ǥ�����",maxcp:465,atk:109,def:88,hp:20}, {no:51,name:"�����ȥꥪ",maxcp:1333,atk:167,def:147,hp:70}, {no:52,name:"�˥㡼��",maxcp:638,atk:92,def:81,hp:80}, {no:53,name:"�ڥ륷����",maxcp:1539,atk:150,def:139,hp:130}, {no:54,name:"�����å�",maxcp:966,atk:122,def:96,hp:100}, {no:55,name:"������å�",maxcp:2270,atk:191,def:163,hp:160}, {no:56,name:"�ޥ�",maxcp:1002,atk:148,def:87,hp:80}, {no:57,name:"�����ꥶ��",maxcp:2105,atk:207,def:144,hp:130}, {no:58,name:"�����ǥ�",maxcp:1110,atk:136,def:96,hp:110}, {no:59,name:"������ǥ�",maxcp:2839,atk:227,def:166,hp:180}, {no:60,name:"�˥����",maxcp:695,atk:101,def:82,hp:80}, {no:61,name:"�˥����",maxcp:1313,atk:130,def:130,hp:130}, {no:62,name:"�˥���ܥ�",maxcp:2441,atk:182,def:187,hp:180}, {no:63,name:"��������",maxcp:1148,atk:195,def:103,hp:50}, {no:64,name:"��顼",maxcp:1859,atk:232,def:138,hp:80}, {no:65,name:"�ա��ǥ���",maxcp:2887,atk:271,def:194,hp:110}, {no:66,name:"���ꥭ��",maxcp:1199,atk:137,def:88,hp:140}, {no:67,name:"�����ꥭ��",maxcp:1910,atk:177,def:130,hp:160}, {no:68,name:"�����ꥭ��",maxcp:2889,atk:234,def:162,hp:180}, {no:69,name:"�ޥ��ĥܥ�",maxcp:916,atk:139,def:64,hp:100}, {no:70,name:"���ĥɥ�",maxcp:1475,atk:172,def:95,hp:130}, {no:71,name:"���ĥܥå�",maxcp:2268,atk:207,def:138,hp:160}, {no:72,name:"��Υ��饲",maxcp:956,atk:97,def:182,hp:80}, {no:73,name:"�ɥ����饲",maxcp:2374,atk:166,def:237,hp:160}, {no:74,name:"�����ĥ֥�",maxcp:1193,atk:132,def:163,hp:80}, {no:75,name:"��������",maxcp:1815,atk:164,def:196,hp:110}, {no:76,name:"�������˥�",maxcp:2916,atk:211,def:229,hp:160}, {no:77,name:"�ݥˡ���",maxcp:1502,atk:170,def:132,hp:100}, {no:78,name:"������å�",maxcp:2252,atk:207,def:167,hp:130}, {no:79,name:"��ɥ�",maxcp:1204,atk:109,def:109,hp:180}, {no:80,name:"��ɥ��",maxcp:2482,atk:177,def:194,hp:190}, {no:81,name:"������",maxcp:1083,atk:165,def:128,hp:50}, {no:82,name:"�쥢������",maxcp:2237,atk:223,def:182,hp:100}, {no:83,name:"����ͥ�",maxcp:1092,atk:124,def:118,hp:104}, {no:84,name:"�ɡ��ɡ�",maxcp:1011,atk:158,def:88,hp:70}, {no:85,name:"�ɡ��ɥꥪ",maxcp:2138,atk:218,def:145,hp:120}, {no:86,name:"�ѥ��復",maxcp:899,atk:85,def:128,hp:130}, {no:87,name:"���奴��",maxcp:1894,atk:139,def:184,hp:180}, {no:88,name:"�٥ȥ٥���",maxcp:1269,atk:135,def:90,hp:160}, {no:89,name:"�٥ȥ٥ȥ�",maxcp:2709,atk:190,def:184,hp:210}, {no:90,name:"���������",maxcp:958,atk:116,def:168,hp:60}, {no:91,name:"�ѥ륷����",maxcp:2475,atk:186,def:323,hp:100}, {no:92,name:"������",maxcp:1002,atk:186,def:70,hp:60}, {no:93,name:"��������",maxcp:1716,atk:223,def:112,hp:90}, {no:94,name:"����",maxcp:2619,atk:261,def:156,hp:120}, {no:95,name:"�����",maxcp:1002,atk:85,def:288,hp:70}, {no:96,name:"�����",maxcp:992,atk:89,def:158,hp:120}, {no:97,name:"����ѡ�",maxcp:2048,atk:144,def:215,hp:170}, {no:98,name:"�����",maxcp:1386,atk:181,def:156,hp:60}, {no:99,name:"���顼",maxcp:2694,atk:240,def:214,hp:110}, {no:100,name:"�ӥ�����",maxcp:857,atk:109,def:114,hp:80}, {no:101,name:"�ޥ�ޥ���",maxcp:1900,atk:173,def:179,hp:120}, {no:102,name:"���ޥ���",maxcp:1102,atk:107,def:140,hp:120}, {no:103,name:"�ʥå���",maxcp:2916,atk:233,def:158,hp:190}, {no:104,name:"���饫��",maxcp:943,atk:90,def:165,hp:100}, {no:105,name:"���饬��",maxcp:1691,atk:144,def:200,hp:120}, {no:106,name:"�����顼",maxcp:2406,atk:224,def:211,hp:100}, {no:107,name:"���ӥ�顼",maxcp:2098,atk:193,def:212,hp:100}, {no:108,name:"�٥����",maxcp:1322,atk:108,def:137,hp:180}, {no:109,name:"�ɥ�����",maxcp:1091,atk:119,def:164,hp:80}, {no:110,name:"�ޥ��ɥ���",maxcp:2183,atk:174,def:221,hp:130}, {no:111,name:"�����ۡ���",maxcp:1679,atk:140,def:157,hp:160}, {no:112,name:"�����ɥ�",maxcp:3300,atk:222,def:206,hp:210}, {no:113,name:"��å���",maxcp:1469,atk:60,def:176,hp:500}, {no:114,name:"����",maxcp:2208,atk:183,def:205,hp:130}, {no:115,name:"���롼��",maxcp:2463,atk:181,def:165,hp:210}, {no:116,name:"���åġ�",maxcp:921,atk:129,def:125,hp:60}, {no:117,name:"�����ɥ�",maxcp:1979,atk:187,def:182,hp:110}, {no:118,name:"�ȥ������",maxcp:1006,atk:123,def:115,hp:90}, {no:119,name:"�����ޥ���",maxcp:2040,atk:175,def:154,hp:160}, {no:120,name:"�ҥȥǥޥ�",maxcp:926,atk:137,def:112,hp:60}, {no:121,name:"�������ߡ�",maxcp:2303,atk:210,def:184,hp:120}, {no:122,name:"�Х�䡼��",maxcp:1984,atk:192,def:233,hp:80}, {no:123,name:"���ȥ饤��",maxcp:2464,atk:218,def:170,hp:140}, {no:124,name:"�롼�����",maxcp:2512,atk:223,def:182,hp:130}, {no:125,name:"����֡�",maxcp:2196,atk:198,def:173,hp:130}, {no:126,name:"�֡��С�",maxcp:2254,atk:206,def:169,hp:130}, {no:127,name:"��������",maxcp:2770,atk:238,def:197,hp:130}, {no:128,name:"������",maxcp:2488,atk:198,def:197,hp:150}, {no:129,name:"��������",maxcp:220,atk:29,def:102,hp:40}, {no:130,name:"�����ɥ�",maxcp:3281,atk:237,def:197,hp:190}, {no:131,name:"��ץ饹",maxcp:2603,atk:165,def:180,hp:260}, {no:132,name:"����",maxcp:718,atk:91,def:91,hp:96}, {no:133,name:"�����֥�",maxcp:969,atk:104,def:121,hp:110}, {no:134,name:"������",maxcp:3157,atk:205,def:177,hp:260}, {no:135,name:"���������",maxcp:2730,atk:232,def:201,hp:130}, {no:136,name:"�֡�������",maxcp:2904,atk:246,def:204,hp:130}, {no:137,name:"�ݥꥴ��",maxcp:1567,atk:153,def:139,hp:130}, {no:138,name:"����ʥ���",maxcp:1345,atk:155,def:174,hp:70}, {no:139,name:"���ॹ����",maxcp:2685,atk:207,def:227,hp:140}, {no:140,name:"���֥�",maxcp:1172,atk:148,def:162,hp:60}, {no:141,name:"���֥ȥץ�",maxcp:2517,atk:220,def:203,hp:120}, {no:142,name:"�ץƥ�",maxcp:2608,atk:221,def:164,hp:160}, {no:143,name:"���ӥ���",maxcp:3355,atk:190,def:190,hp:320}, {no:144,name:"�ե����",maxcp:2933,atk:192,def:249,hp:180}, {no:145,name:"�������",maxcp:3330,atk:253,def:188,hp:180}, {no:146,name:"�ե����䡼",maxcp:3272,atk:251,def:184,hp:180}, {no:147,name:"�ߥ˥�奦",maxcp:860,atk:119,def:94,hp:82}, {no:148,name:"�ϥ���塼",maxcp:1609,atk:163,def:138,hp:122}, {no:149,name:"������塼",maxcp:3581,atk:263,def:201,hp:182}, {no:150,name:"�ߥ奦�ġ�",maxcp:4760,atk:330,def:200,hp:212}, {no:151,name:"�ߥ奦",maxcp:3090,atk:210,def:209,hp:200}, {no:152,name:"�������",maxcp:801,atk:92,def:122,hp:90}, {no:153,name:"�٥����",maxcp:1296,atk:122,def:155,hp:120}, {no:154,name:"�ᥬ�˥���",maxcp:2227,atk:168,def:202,hp:160}, {no:155,name:"�ҥΥ��饷",maxcp:831,atk:116,def:96,hp:78}, {no:156,name:"�ޥ��ޥ饷",maxcp:1484,atk:158,def:129,hp:116}, {no:157,name:"�Х��ա���",maxcp:2686,atk:223,def:176,hp:156}, {no:158,name:"��˥Υ�",maxcp:1011,atk:117,def:116,hp:100}, {no:159,name:"���ꥲ����",maxcp:1598,atk:150,def:151,hp:130}, {no:160,name:"����������",maxcp:2721,atk:205,def:197,hp:170}, {no:161,name:"������",maxcp:519,atk:79,def:77,hp:70}, {no:162,name:"��������",maxcp:1667,atk:148,def:130,hp:170}, {no:163,name:"�ۡ��ۡ�",maxcp:640,atk:67,def:101,hp:120}, {no:164,name:"���Υ���",maxcp:2040,atk:145,def:179,hp:200}, {no:165,name:"��ǥ���",maxcp:663,atk:72,def:142,hp:80}, {no:166,name:"��ǥ�����",maxcp:1275,atk:107,def:209,hp:110}, {no:167,name:"���ȥޥ�",maxcp:685,atk:105,def:73,hp:80}, {no:168,name:"���ꥢ�ɥ�",maxcp:1636,atk:161,def:128,hp:140}, {no:169,name:"�����Хå�",maxcp:2466,atk:194,def:178,hp:170}, {no:170,name:"��������",maxcp:1067,atk:106,def:106,hp:150}, {no:171,name:"�����",maxcp:2077,atk:146,def:146,hp:250}, {no:172,name:"�ԥ��塼",maxcp:376,atk:77,def:63,hp:40}, {no:173,name:"�ԥ�",maxcp:620,atk:75,def:91,hp:100}, {no:174,name:"�ץץ��",maxcp:512,atk:69,def:34,hp:180}, {no:175,name:"�ȥ��ԡ�",maxcp:540,atk:67,def:116,hp:70}, {no:176,name:"�ȥ����å�",maxcp:1543,atk:139,def:191,hp:110}, {no:177,name:"�ͥ��ƥ�",maxcp:925,atk:134,def:89,hp:80}, {no:178,name:"�ͥ��ƥ���",maxcp:1975,atk:192,def:146,hp:130}, {no:179,name:"����",maxcp:887,atk:114,def:82,hp:110}, {no:180,name:"�⥳��",maxcp:1402,atk:145,def:112,hp:140}, {no:181,name:"�ǥ��奦",maxcp:2695,atk:211,def:172,hp:180}, {no:182,name:"���쥤�ϥ�",maxcp:2108,atk:169,def:189,hp:150}, {no:183,name:"�ޥ��",maxcp:420,atk:37,def:93,hp:140}, {no:184,name:"�ޥ���",maxcp:1503,atk:112,def:152,hp:200}, {no:185,name:"�����å���",maxcp:2065,atk:167,def:198,hp:140}, {no:186,name:"�˥���ȥ�",maxcp:2371,atk:174,def:192,hp:180}, {no:187,name:"�ϥͥå�",maxcp:508,atk:67,def:101,hp:70}, {no:188,name:"�ݥݥå�",maxcp:882,atk:91,def:127,hp:110}, {no:189,name:"�勵�å�",maxcp:1553,atk:118,def:197,hp:150}, {no:190,name:"�����ѥ�",maxcp:1188,atk:136,def:112,hp:110}, {no:191,name:"�ҥޥʥå�",maxcp:316,atk:55,def:55,hp:60}, {no:192,name:"���ޥ��",maxcp:2048,atk:185,def:148,hp:150}, {no:193,name:"������",maxcp:1326,atk:154,def:94,hp:130}, {no:194,name:"���ѡ�",maxcp:596,atk:75,def:75,hp:110}, {no:195,name:"�̥���",maxcp:1929,atk:152,def:152,hp:190}, {no:196,name:"�����ե�",maxcp:3000,atk:261,def:194,hp:130}, {no:197,name:"�֥�å���",maxcp:2052,atk:126,def:250,hp:190}, {no:198,name:"��ߥ��饹",maxcp:1392,atk:175,def:87,hp:120}, {no:199,name:"��ɥ���",maxcp:2482,atk:177,def:194,hp:190}, {no:200,name:"�०��",maxcp:1781,atk:167,def:167,hp:120}, {no:201,name:"����Ρ���",maxcp:1022,atk:136,def:91,hp:96}, {no:202,name:"�����ʥ�",maxcp:1024,atk:60,def:106,hp:380}, {no:203,name:"�����ꥭ",maxcp:1863,atk:182,def:133,hp:140}, {no:204,name:"���̥�����",maxcp:1045,atk:108,def:146,hp:100}, {no:205,name:"�ե���ȥ�",maxcp:2263,atk:161,def:242,hp:150}, {no:206,name:"�Υ��å�",maxcp:1615,atk:131,def:131,hp:200}, {no:207,name:"���饤����",maxcp:1758,atk:143,def:204,hp:130}, {no:208,name:"�ϥ��͡���",maxcp:2439,atk:148,def:333,hp:150}, {no:209,name:"�֥롼",maxcp:1124,atk:137,def:89,hp:120}, {no:210,name:"�����֥�",maxcp:2440,atk:212,def:137,hp:180}, {no:211,name:"�ϥ����",maxcp:1910,atk:184,def:148,hp:130}, {no:212,name:"�ϥå���",maxcp:2801,atk:236,def:191,hp:140}, {no:213,name:"�ĥܥĥ�",maxcp:300,atk:17,def:396,hp:40}, {no:214,name:"�إ饯����",maxcp:2938,atk:234,def:189,hp:160}, {no:215,name:"�˥塼��",maxcp:1868,atk:189,def:157,hp:110}, {no:216,name:"�ҥᥰ��",maxcp:1184,atk:142,def:93,hp:120}, {no:217,name:"���",maxcp:2760,atk:236,def:144,hp:180}, {no:218,name:"�ޥ��ޥå�",maxcp:750,atk:118,def:71,hp:80}, {no:219,name:"�ޥ����르",maxcp:1543,atk:139,def:209,hp:100}, {no:220,name:"����ࡼ",maxcp:663,atk:90,def:74,hp:100}, {no:221,name:"���Υࡼ",maxcp:2284,atk:181,def:147,hp:200}, {no:222,name:"���ˡ���",maxcp:1214,atk:118,def:156,hp:110}, {no:223,name:"�ƥåݥ���",maxcp:749,atk:127,def:69,hp:70}, {no:224,name:"��������",maxcp:2124,atk:197,def:141,hp:150}, {no:225,name:"�ǥ�С���",maxcp:937,atk:128,def:90,hp:90}, {no:226,name:"�ޥ���",maxcp:2032,atk:148,def:260,hp:130}, {no:227,name:"���������",maxcp:2032,atk:148,def:260,hp:130}, {no:228,name:"�ǥ�ӥ�",maxcp:1110,atk:152,def:93,hp:90}, {no:229,name:"�إ륬��",maxcp:2529,atk:224,def:159,hp:150}, {no:230,name:"���ɥ�",maxcp:2424,atk:194,def:194,hp:150}, {no:231,name:"���ޥ���",maxcp:1175,atk:107,def:107,hp:180}, {no:232,name:"�ɥ�ե���",maxcp:3022,atk:214,def:214,hp:180}, {no:233,name:"�ݥꥴ��2",maxcp:2546,atk:198,def:183,hp:170}, {no:234,name:"���ɥ���",maxcp:1988,atk:192,def:132,hp:146}, {no:235,name:"�ɡ��֥�",maxcp:389,atk:40,def:88,hp:110}, {no:236,name:"�Х륭��",maxcp:404,atk:64,def:64,hp:70}, {no:237,name:"���ݥ��顼",maxcp:1905,atk:173,def:214,hp:100}, {no:238,name:"����塼��",maxcp:1230,atk:153,def:116,hp:90}, {no:239,name:"���쥭�å�",maxcp:1073,atk:135,def:110,hp:90}, {no:240,name:"�֥ӥ�",maxcp:1178,atk:151,def:108,hp:90}, {no:241,name:"�ߥ륿��",maxcp:2312,atk:157,def:211,hp:190}, {no:242,name:"�ϥԥʥ�",maxcp:3219,atk:129,def:229,hp:510}, {no:243,name:"�饤����",maxcp:3349,atk:241,def:210,hp:180}, {no:244,name:"����ƥ�",maxcp:3377,atk:235,def:176,hp:230}, {no:245,name:"��������",maxcp:2823,atk:180,def:235,hp:200}, {no:246,name:"�衼���饹",maxcp:904,atk:115,def:93,hp:100}, {no:247,name:"���ʥ��饹",maxcp:1608,atk:155,def:133,hp:140}, {no:248,name:"�Х饹",maxcp:3670,atk:251,def:212,hp:200}, {no:249,name:"�륮��",maxcp:3598,atk:193,def:323,hp:212}, {no:250,name:"�ۥ�����",maxcp:4650,atk:263,def:301,hp:212}, {no:251,name:"����ӥ�",maxcp:3090,atk:210,def:210,hp:200}, ]; // �ݥ����̾�ܥ�����ֹ��ޤ���̾������¤٤�ɽ�� var changetbl = function(mode){ var len = pktbl.length; var div = document.getElementById("namediv"); while (div.firstChild){ div.removeChild(div.firstChild); } if (mode == 0){ pktbl.sort(function(a,b){ if (a.no > b.no) return 1; if (a.no < b.no) return -1; return 0; }); }else if (mode == 1){ pktbl.sort(function(a,b){ if (a.name > b.name) return 1; if (a.name < b.name) return -1; return 0; }); } for (var i=0; i<len; i++){ var inp = document.createElement("input"); inp.type = "button"; inp.value = pktbl[i].name; if (pktbl[i].no < 152){ inp.style.backgroundColor = "#8ca"; }else{ inp.style.backgroundColor = "#c8a"; } inp.onclick = function(e){setname(this.value);}; div.appendChild(inp); } }; // �������ƤΥ��ꥢ var clearinp = function(mode){ var elm = null; if (mode){ elm = document.getElementById("pkname"); elm.value = ""; elm = document.getElementById("pk_cp"); elm.value = ""; elm = document.getElementById("pk_hp"); elm.value = ""; elm = document.getElementById("selsand"); elm.selectedIndex = 0; } elm = document.getElementById("pk_choice1_1"); elm.checked = false; elm = document.getElementById("pk_choice1_2"); elm.checked = false; elm = document.getElementById("pk_choice1_3"); elm.checked = false; elm = document.getElementById("pk_choice1_4"); elm.checked = false; elm = document.getElementById("pk_choice2_1"); elm.checked = false; elm = document.getElementById("pk_choice2_2"); elm.checked = false; elm = document.getElementById("pk_choice2_3"); elm.checked = false; elm = document.getElementById("pk_choice2_4"); elm.checked = false; elm = document.getElementById("pk_choice3_1"); elm.checked = false; elm = document.getElementById("pk_choice3_2"); elm.checked = false; elm = document.getElementById("pk_choice3_3"); elm.checked = false; elm = document.getElementById("answer"); while (elm.firstChild){ elm.removeChild(elm.firstChild); } }; // ������� var init = function(){ changetbl(0); }; // �ݥ����ܥ������줿�Ȥ��ƤФ�� var setname = function(name){ var inp = document.getElementById("pkname"); inp.value = name; inp = document.getElementById("pk_cp"); inp.focus(); }; // ���ϥ����å� var precheck = function(cp, hp, sand){ var str = "�����ʤ�"; var n = pktbl.length; var inp = document.getElementById("pkname"); var pid = -1; for (var i=0; i<n; i++){ if (inp.value == pktbl[i].name){ pid = i; break; } } if (pid < 0){ str = "�ݥ��������Ʋ�������" }else{ if (!sand){ str = "������ɬ�פ����κ������Ʋ�������" pid = -1; } if (!hp){ str = "HP��Ⱦ�ѿ��������Ϥ��Ʋ�������" pid = -1; } if (!cp){ str = "CP��Ⱦ�ѿ��������Ϥ��Ʋ�������" pid = -1; } } return {pid:pid, str:str}; }; // CP�� var cpcalc = function(p_atk, p_def, p_hp, m_atk, m_def, m_hp, m_c){ return parseInt((p_atk+m_atk)*Math.sqrt(p_def+m_def)*Math.sqrt(p_hp+m_hp)*m_c*m_c/10.0); }; // �������ᥤ�� var calcmain = function(pid, cp, hp, sand, k1, k2, k2f, ares){ var atk_range = {min:0, max:15}; // ������ �� var def_range = {min:0, max:15}; // �ɸ��� �� var hp_range = {min:0, max:15}; // ���ϥ�� �� var kotai1 = [ // �������������ɾ�� {min:37, max:45}, {min:30, max:36}, {min:23, max:29}, {min:0, max:22} ]; var kotai2 = [ // ��������������ɾ�� {min:15, max:15}, {min:13, max:14}, {min:8, max:12}, {min:0, max:7} ]; var m = mltbl.length; var ahp = []; var batk = parseInt(pktbl[pid].atk); // ��²�� ���� var bdef = parseInt(pktbl[pid].def); // ��²�� �ɸ� var bhp = parseInt(pktbl[pid].hp); // ��²�� ���� if (k2){ if (k2f & 1){ // ����ɾ�� ����ON atk_range = kotai2[k2-1]; def_range.max = kotai2[k2-1].max; hp_range.max = kotai2[k2-1].max; } if (k2f & 2){ // ����ɾ�� �ɸ�ON def_range = kotai2[k2-1]; atk_range.max = kotai2[k2-1].max; hp_range.max = kotai2[k2-1].max; } if (k2f & 4){ // ����ɾ�� ����ON hp_range = kotai2[k2-1]; atk_range.max = kotai2[k2-1].max; def_range.max = kotai2[k2-1].max; } } // Ϳ����줿�ѥ����˹��פ���ȣФȥݥ�����٥�Υڥ���������� �� for (var i=hp_range.min; i<=hp_range.max; i++){ for (var j=0; j<m-1; j++){ if (mltbl[j+1].sand == sand){ var thp = parseInt((bhp+i) * mltbl[j].c); if (thp == hp){ ahp.push({hp:i, mli:j}); } } } } for (var i=0; i<ahp.length; i++){ // �ȣХ롼�� var mlt = mltbl[ahp[i].mli]; for (var j=atk_range.min; j<=atk_range.max; j++){ // ����롼�� for (var k=def_range.min; k<=def_range.max; k++){ // �ɸ�롼�� // CP�� var t = cpcalc(j,k,ahp[i].hp, batk,bdef,bhp, mlt.c); if (t == cp){ // CP���� var h = ahp[i].hp; // j:����, k:�ɸ�, h:���� var tot = j+k+h; if (k1){ // ��פ����ɾ������������ if (tot < kotai1[k1-1].min || kotai1[k1-1].max < tot){ continue; } } if (k2){ // ���⤬��2ɾ���ϰϤ��������Ƥ��뤫 if (j < atk_range.min || atk_range.max < j){ continue; } // �ɸ椬��2ɾ���ϰϤ��������Ƥ��뤫 if (k < def_range.min || def_range.max < k){ continue; } // ���Ϥ���2ɾ���ϰϤ��������Ƥ��뤫 if (h < hp_range.min || hp_range.max < h){ continue; } // ����Τߥ����å��λ������� > �ɸ�,���ϤǤ��뤳�� if (k2f == 1 && (j <= k || j <= h)){ continue; } // �ɸ�Τߥ����å��λ����ɸ� > ����,���ϤǤ��뤳�� if (k2f == 2 && (k <= j || k <= h)){ continue; } // ���ϤΤߥ����å��λ������� > ����,�ɸ�Ǥ��뤳�� if (k2f == 4 && (h <= j || h <= k)){ continue; } // ����/�ɸ�����å��λ���������ɸ椫�ġ���������ϤǤ��뤳�� if (k2f == 3 && (j != k || j <= h)){ continue; } // ����/���ϥ����å��λ�����������Ϥ��ġ�������ɸ�Ǥ��뤳�� if (k2f == 5 && (j != h || j <= k)){ continue; } // �ɸ�/���ϥ����å��λ����ɸ�����Ϥ��ġ��ɸ�乶��Ǥ��뤳�� if (k2f == 6 && (k != h || k <= j)){ continue; } // ����/�ɸ�/���ϥ����å��λ���������ɸ�����ϤǤ��뤳�� if (k2f == 7 && (j != k || j != h)){ continue; } } // ������ɲ�, {��, ��٥�, ����, �ɸ�, �ȣ�} ares.push({per:tot/45, ml:mlt.ml, atk:j, def:k, hp:h}); } } } } }; // ���ܥ������줿�Ȥ��ƤФ�� var calc = function(){ var cp = parseInt(document.getElementById("pk_cp").value); var hp = parseInt(document.getElementById("pk_hp").value); var sel = document.getElementById("selsand"); var sand = parseInt( sel.options[sel.selectedIndex].value); var pchk = precheck(cp, hp, sand); // ���ϥ����å� var ares = []; var answerstr = pchk.str; var div = document.getElementById("answer"); var k1 = parseInt(hyouka.pk_choice1.value); var k2 = parseInt(hyouka.pk_choice2.value); var k2f = 0; if (k2){ if (hyouka.pk_choice3a.checked){ k2f |= 1; } if (hyouka.pk_choice3b.checked){ k2f |= 2; } if (hyouka.pk_choice3c.checked){ k2f |= 4; } } if (pchk.pid >= 0){ // �����ᥤ�� ares����˷�̤��֤� calcmain(pchk.pid, cp, hp, sand, k1, k2, k2f, ares); if (ares.length){ // ���ͥ�褷�ƹ߽祽���� ares.sort(function(a,b){ if (a.per < b.per) return 1; if (a.per > b.per) return -1; if (a.ml < b.ml) return 1; if (a.ml > b.ml) return -1; return 0; }); // ��̤�ơ��֥�η������� answerstr = "<table border='1'><tr><th>��</th><th>Lv</th><th>����</th><th>�ɸ�</th><th>�ȣ�</th></tr>"; for (var i=0; i<ares.length; i++){ answerstr += "<tr><td>" + Math.round(ares[i].per * 10000) / 100 + "</td><td>" + ares[i].ml + "</td><td>" + ares[i].atk + "</td><td>" + ares[i].def + "</td><td>" + ares[i].hp + "</td></tr>"; } answerstr += "</table>"; } } div.innerHTML = answerstr; }; </script> </head> <body onload="init();"> �����ͷ��ġ��롡 <input class="pk_choice1" type="radio" name="btn_choice" value="0" checked="checked" onclick="changetbl(0);">�ֹ�硡 <input class="pk_choice1" type="radio" name="btn_choice" value="1" onclick="changetbl(1);">̾���� <br /> <div id="namediv"></div> <br /> <span class="inp_lavel">Name </span><input id="pkname" class="pk_inp" type="text" value="" readonly="true"> <span class="inp_lavel">CP </span><input id="pk_cp" class="pk_inp" type="text" value=""> <span class="inp_lavel">HP </span><input id="pk_hp" class="pk_inp" type="text" value=""> <select id="selsand"> <option value="0">������ɬ�פ����κ�</option> <option value="200">200</option> <option value="400">400</option> <option value="600">600</option> <option value="800">800</option> <option value="1000">1000</option> <option value="1300">1300</option> <option value="1600">1600</option> <option value="1900">1900</option> <option value="2200">2200</option> <option value="2500">2500</option> <option value="3000">3000</option> <option value="3500">3500</option> <option value="4000">4000</option> <option value="4500">4500</option> <option value="5000">5000</option> <option value="6000">6000</option> <option value="7000">7000</option> <option value="8000">8000</option> <option value="9000">9000</option> <option value="10000">10000</option> </select> <br /> <br /> <form class="hyouka" name="hyouka"> ���ɾ��<br /> <input id="pk_choice1_1" class="pk_choice1" type="radio" name="pk_choice1" value="1">1st <input id="pk_choice1_2" class="pk_choice1" type="radio" name="pk_choice1" value="2">2nd <input id="pk_choice1_3" class="pk_choice1" type="radio" name="pk_choice1" value="3">3rd <input id="pk_choice1_4" class="pk_choice1" type="radio" name="pk_choice1" value="4">4th <br /> ����ɾ��<br /> <div> <input id="pk_choice2_1" class="pk_choice2" type="radio" name="pk_choice2" value="1">1st <input id="pk_choice2_2" class="pk_choice2" type="radio" name="pk_choice2" value="2">2nd <input id="pk_choice2_3" class="pk_choice2" type="radio" name="pk_choice2" value="3">3rd <input id="pk_choice2_4" class="pk_choice2" type="radio" name="pk_choice2" value="4">4th <br /> <input id="pk_choice3_1" class="pk_choice3" type="checkbox" name="pk_choice3a" value="1">���� <input id="pk_choice3_2" class="pk_choice3" type="checkbox" name="pk_choice3b" value="2">�ɸ� <input id="pk_choice3_3" class="pk_choice3" type="checkbox" name="pk_choice3c" value="3">�ȣ� </div> </form> <br /> <input type="button" value="���ס�����" onclick="calc(); return false;"> <input type="button" value="��ɾ�����ꥢ��" onclick="clearinp(false); return false;"> <input type="button" value="��ALL���ꥢ��" onclick="clearinp(true); return false;"> <br /> <br /> <hr> <div id="answer"> </div> </body> </html>
Tags: �ץ��������
author : HUNDREDSOFT | - | -









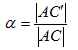
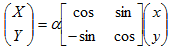


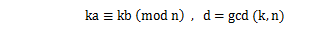 �ʤ��
�ʤ��