2Dʿ�̤Dz�ˡ������Ȥ�
| �ץ�������� | 2013/07/28 Sun 06:13
���Ѵؿ��β�ˡ������¸���Ǥ��礦����
��ο��ؤǽ�����ĤǤ���
�������Ƥ⡢�ºݤΥץ������ǤλȤ�����ͭ���������Ĥ��뤳�Ȥϳ�̵�˶ᤤ��
�ޤ�ǡ����ػ�Τ�������ˤ���褦�Ǥ���
���β�ž��Ϣ³���륱�����Ǥϡ����٤��ݻ�����ץ�����ब�ۤȤ�ɤǤ���
���������������ä��������Ǥϡ�sin, cos �ͤ���¸���Ƥ�����������
if ʸ�����ʤ��ʤꡢ�Զ�礬���ʤ��ʤä��ꤷ�ޤ���
-------
������ABCD�����ä��Ȥ��ơ�A�������ˤ���C����ư������
�Ѳ���ζ��AB��C��D�� ����롣
â��������νIJ����Aspect��ˤ��Ѥ��ʤ���ΤȤ��롣
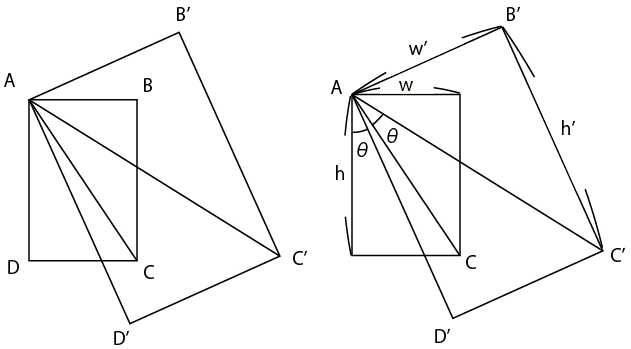
����γ���Ψ(��)�ϡ������ǵ�ޤ롣
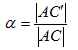
���ζ�������ȹ⤵�줾�졢w,h�Ȥ����Ѳ�������ȹ⤵��w��,h�� �Ȥ��롣
�ޤ�����ž�Ѥ�� �Ȥ��롣
A,C�� �ϴ��ΤǤ���Τǡ�B�� ��D�� �Τ����줫���狼����ɤ���
���Ĥ�����ˡ���ͤ����뤬��
ñ��ʤΤϡ�����Ψ(��)�Ȳ�ž��(��) ����ơ����ι�����������Ʒ�������ˡ��������
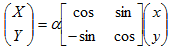
������ˡ�η����ϡ��� ����������ξݸ¤ˤ����ơ�������ɬ�פˤʤ뤳�Ȥ�������
�㤨��atan�Ǥϡ�(-��/2 �� �� �� ��/2)���ϰϤǤ�������������ޤ餺��
acos�Ǥ�(0 �� �� �� ��)���ϰϤǤ�����ޤ�ʤ���
C�� ��A�����濴�˲�ž������Ȥ狼��䤹����
������ˡ�ϰճ��ȴְ㤤���Ȥ��䤹�����ƥ��ȥ�������������Τǡ����٤��ǤϤʤ���
A,C,C�� �κ�ɸ���狼�äƤ���Τǡ�
�٥��ȥ�AC��AC�� �����Ѥȳ��Ѥ���cos��,sin�� �Ф��롣
���Ѥθ���
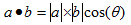
���Ѥθ���
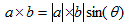
����Υ����������ƤϤᡢcos,sin��ȡ�
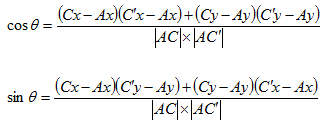
HTML5��canvas���饹�Ǥϡ�Context.transform�ǹ���黻����ǽ�ʤΤ�
���Υѥ�(cos,sin,-sin,cos)����ꤹ����ɤ���
���ٲ�ž�����ơ��夫�鹹�˲�ž���ɲä������ͤ��롣
�ޤǤϡ�C�� ����C'�� ������������ư�����Ȥ��롣
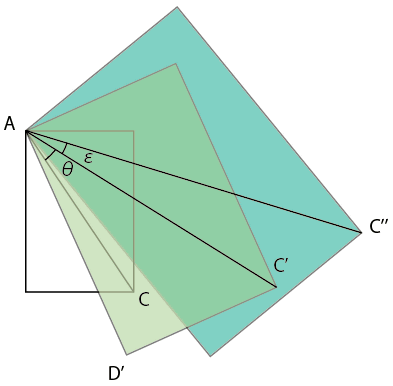
�ޤ����Ф���ˡ�ǡ��٥��ȥ�AC�ǡ�AC'�� �����Ѥȳ��Ѥ���cos(��),sin(��)�Ф��롣
���˦� ��ž���Ƥ��ơ����˦� �β�ž���ä��Ȥ���ȡ���ˡ�����ˤ��
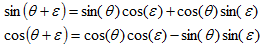
����Ψ��Ʊ�ͤˡ����˳���Ψ�� �Ǥ��ꡢ
����˳���Ψ�� ���ä��Ȥ���С��£��� ����������Ψ�ˤʤ롣
����ȯŸ�����ơ�����̾���ž����³Ū��Ϣ³ȯ�����륱������ͤ��Ƥߤޤ���
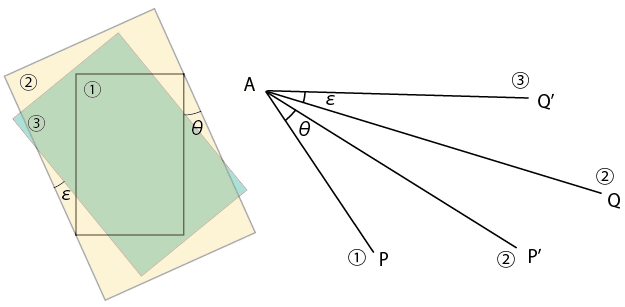
����ץ��¹Ԥ����Ȥ狼��䤹����
���Ȥ��Ƥϡ�
A����Canvas������Ȥ��ơ�����å�����P�Ȥ��롣
�����������λ����̤ˤϡ����ζ����ɽ������Ƥ��롣
���θ塢���磻������P�� �ޤǰ�ư���������ǻؤ�Υ����
�����������λ����̤ˤϡ����ζ����ɽ������Ƥ��롣
�Ƥӡ�Q���ǥ���å���Ԥ���
�����������λ����̤ˤϡ����ζ����ɽ������Ƥ��롣
���磻�פ�Q�� �ޤǰ�ư���ؤ�Υ����
�����������λ����̤ˤϡ����ζ����ɽ������Ƥ��롣
�¸���ˡ�Ϥ����������뤬��
���磻��OFF���ˡ����λ����γ���Ψ(��x��)����ž����(sin(��+��),cos(��+��))����¸���Ƥ�����
����å����ˡ��¡��x��, sin(��)��sin(��+��), cos(��)��cos(��+��)
�Ȥ��ƺƳ��Ϥ�����ɤ���
Javascript�ǤΥ����������ɤϼ��Τ褦�ˤʤ롣
�ճ������ݤʽ����Ǥ����������ɤ��̤ꡢ�黻������ifʸ�ϰ�Ĥ⤢��ޤ���
������ˡ�������ϡ������ѿ��λ��Ѥ����ʤ����ȡ��� ������ʤ��ʻ��Ѵؿ��θ����ϻȤäƤ��ޤ����� �ؿ��Ȥ��Ƥ�sin��cos �ϻȤäƤ��ʤ����ȤäƤ���Τϲø�����ȥ롼�ȤΤߡ��ˤ��Ȥǡ�if ʸ��ʤ���������ޤ���
�¹ԥ���ץ�Ϥ�����
IE9�ʹ�/Chrome/Safari/FF/Android�ǡ���ǧ���Ƥ��ޤ���
Tags: �ץ��������
��ο��ؤǽ�����ĤǤ���
�������Ƥ⡢�ºݤΥץ������ǤλȤ�����ͭ���������Ĥ��뤳�Ȥϳ�̵�˶ᤤ��
�ޤ�ǡ����ػ�Τ�������ˤ���褦�Ǥ���
���β�ž��Ϣ³���륱�����Ǥϡ����٤��ݻ�����ץ�����ब�ۤȤ�ɤǤ���
���������������ä��������Ǥϡ�sin, cos �ͤ���¸���Ƥ�����������
if ʸ�����ʤ��ʤꡢ�Զ�礬���ʤ��ʤä��ꤷ�ޤ���
-------
������ABCD�����ä��Ȥ��ơ�A�������ˤ���C����ư������
�Ѳ���ζ��AB��C��D�� ����롣
â��������νIJ����Aspect��ˤ��Ѥ��ʤ���ΤȤ��롣

����γ���Ψ(��)�ϡ������ǵ�ޤ롣
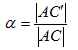
���ζ�������ȹ⤵�줾�졢w,h�Ȥ����Ѳ�������ȹ⤵��w��,h�� �Ȥ��롣
�ޤ�����ž�Ѥ�� �Ȥ��롣
A,C�� �ϴ��ΤǤ���Τǡ�B�� ��D�� �Τ����줫���狼����ɤ���
���Ĥ�����ˡ���ͤ����뤬��
ñ��ʤΤϡ�����Ψ(��)�Ȳ�ž��(��) ����ơ����ι�����������Ʒ�������ˡ��������
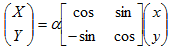
������ˡ�η����ϡ��� ����������ξݸ¤ˤ����ơ�������ɬ�פˤʤ뤳�Ȥ�������
�㤨��atan�Ǥϡ�(-��/2 �� �� �� ��/2)���ϰϤǤ�������������ޤ餺��
acos�Ǥ�(0 �� �� �� ��)���ϰϤǤ�����ޤ�ʤ���
C�� ��A�����濴�˲�ž������Ȥ狼��䤹����
������ˡ�ϰճ��ȴְ㤤���Ȥ��䤹�����ƥ��ȥ�������������Τǡ����٤��ǤϤʤ���
A,C,C�� �κ�ɸ���狼�äƤ���Τǡ�
�٥��ȥ�AC��AC�� �����Ѥȳ��Ѥ���cos��,sin�� �Ф��롣
���Ѥθ���
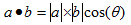
���Ѥθ���
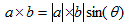
����Υ����������ƤϤᡢcos,sin��ȡ�
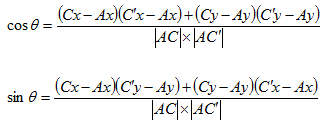
HTML5��canvas���饹�Ǥϡ�Context.transform�ǹ���黻����ǽ�ʤΤ�
���Υѥ�(cos,sin,-sin,cos)����ꤹ����ɤ���
���ٲ�ž�����ơ��夫�鹹�˲�ž���ɲä������ͤ��롣
�ޤǤϡ�C�� ����C'�� ������������ư�����Ȥ��롣

�ޤ����Ф���ˡ�ǡ��٥��ȥ�AC�ǡ�AC'�� �����Ѥȳ��Ѥ���cos(��),sin(��)�Ф��롣
���˦� ��ž���Ƥ��ơ����˦� �β�ž���ä��Ȥ���ȡ���ˡ�����ˤ��
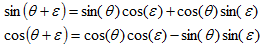
����Ψ��Ʊ�ͤˡ����˳���Ψ�� �Ǥ��ꡢ
����˳���Ψ�� ���ä��Ȥ���С��£��� ����������Ψ�ˤʤ롣
����ȯŸ�����ơ�����̾���ž����³Ū��Ϣ³ȯ�����륱������ͤ��Ƥߤޤ���

����ץ��¹Ԥ����Ȥ狼��䤹����
���Ȥ��Ƥϡ�
A����Canvas������Ȥ��ơ�����å�����P�Ȥ��롣
�����������λ����̤ˤϡ����ζ����ɽ������Ƥ��롣
���θ塢���磻������P�� �ޤǰ�ư���������ǻؤ�Υ����
�����������λ����̤ˤϡ����ζ����ɽ������Ƥ��롣
�Ƥӡ�Q���ǥ���å���Ԥ���
�����������λ����̤ˤϡ����ζ����ɽ������Ƥ��롣
���磻�פ�Q�� �ޤǰ�ư���ؤ�Υ����
�����������λ����̤ˤϡ����ζ����ɽ������Ƥ��롣
�¸���ˡ�Ϥ����������뤬��
���磻��OFF���ˡ����λ����γ���Ψ(��x��)����ž����(sin(��+��),cos(��+��))����¸���Ƥ�����
����å����ˡ��¡��x��, sin(��)��sin(��+��), cos(��)��cos(��+��)
�Ȥ��ƺƳ��Ϥ�����ɤ���
Javascript�ǤΥ����������ɤϼ��Τ褦�ˤʤ롣
<!DOCTYPE html> <html> <!-- // (c)Hundredsoft Corporation. 2013 All right reserved. // // UTF-8����¸���Ʋ����� --> <head> <meta http-equiv="Content-Type" content="text/html; charset=utf-8" /> <meta http-equiv="X-UA-Compatible" content="IE=edge" /> <meta name="viewport" content="width=device-width, initial-scale=1.0, user-scalable=no" /> <title>����̾���ž</title> <script type="text/javascript"> new function() { var m_img = new Image(); var m_ctx = null; var m_O = null; var m_baseX = 0; var m_baseY = 0; var m_cos = 1; var m_sin = 0; var m_prop = 1; var m_Lcos = 1; var m_Lsin = 0; var m_Lprop = 1; var mmove = function(x, y){ // Click��ɸ-�濴 �٥��ȥ� var vx0 = m_baseX - m_O.x; var vy0 = m_baseY - m_O.y; var r0 = Math.sqrt(vx0*vx0 + vy0*vy0); // ���磻��ɸ-�濴 �٥��ȥ� var vx1 = x - m_O.x; var vy1 = y - m_O.y; var r1 = Math.sqrt(vx1*vx1 + vy1*vy1); var cos = (vx0*vx1 + vy0*vy1) / (r0*r1); // ���Ѥ��� var sin = (vx0*vy1 - vy0*vx1) / (r0*r1); // ���Ѥ��� var prop = r1 / r0; draw(prop, cos, sin); }; var draw = function(prop, cos, sin){ m_Lcos = m_cos*cos - m_sin*sin; // ��ˡ����(cos) m_Lsin = m_sin*cos + m_cos*sin; // ��ˡ����(sin) m_Lprop = m_prop * prop; // ����Ψ�β�ˡ�Ͼ褸����� m_ctx.clearRect(0, 0, m_O.x*2, m_O.y*2); m_ctx.save(); // ����� m_ctx.transform( m_Lcos*m_Lprop, m_Lsin*m_Lprop, -m_Lsin*m_Lprop, m_Lcos*m_Lprop, m_O.x, m_O.y); // ��˲����濴�����˰�ư(Ŭ�ѽ������) m_ctx.transform(1, 0, 0, 1, -m_img.width/2, -m_img.height/2); m_ctx.drawImage(m_img, 0, 0); m_ctx.restore(); }; test1 = { init: function(){ var mouseDown = false; var canvas = document.getElementById('c'); canvas.addEventListener('touchstart', function(e) { e.preventDefault(); mouseDown = true; var n = e.touches.length; var rect=e.target.getBoundingClientRect(); m_baseX = e.touches[n-1].pageX-rect.left; m_baseY = e.touches[n-1].pageY-rect.top; m_cos = m_Lcos; m_sin = m_Lsin; m_prop = m_Lprop; }, false); canvas.addEventListener('mousedown', function(e) { e.preventDefault(); mouseDown = true; var rect=e.target.getBoundingClientRect(); m_baseX = e.clientX-rect.left; m_baseY = e.clientY-rect.top; m_cos = m_Lcos; m_sin = m_Lsin; m_prop = m_Lprop; }, false); canvas.addEventListener('touchend', function(e) {mouseDown = false;}, false); canvas.addEventListener('mouseup', function(e) {mouseDown = false;}, false); canvas.addEventListener('touchmove', function (e) { e.preventDefault(); var rect = e.target.getBoundingClientRect(); if (mouseDown) { var n = e.touches.length; mmove(e.touches[n-1].pageX-rect.left, e.touches[n-1].pageY-rect.top); } }, false); canvas.addEventListener('mousemove', function (e) { e.preventDefault(); var rect = e.target.getBoundingClientRect(); if (mouseDown) { mmove(e.clientX-rect.left, e.clientY-rect.top); } }, false); m_img.onload = (function(){ m_O = {x: canvas.width/2, y: canvas.height/2}; m_ctx = canvas.getContext("2d"); draw(1, 1 ,0); }); m_img.width = 260; m_img.height = 390; m_img.src = "test.jpg"; } } }; </script> </head> <body onload="test1.init()"> <canvas id="c" width="640" height="640" style="background-color:#e0e0e0;"> </canvas> </body> </html>
�ճ������ݤʽ����Ǥ����������ɤ��̤ꡢ�黻������ifʸ�ϰ�Ĥ⤢��ޤ���
������ˡ�������ϡ������ѿ��λ��Ѥ����ʤ����ȡ��� ������ʤ��ʻ��Ѵؿ��θ����ϻȤäƤ��ޤ����� �ؿ��Ȥ��Ƥ�sin��cos �ϻȤäƤ��ʤ����ȤäƤ���Τϲø�����ȥ롼�ȤΤߡ��ˤ��Ȥǡ�if ʸ��ʤ���������ޤ���
�¹ԥ���ץ�Ϥ�����
IE9�ʹ�/Chrome/Safari/FF/Android�ǡ���ǧ���Ƥ��ޤ���
Tags: �ץ��������
author : HUNDREDSOFT | - | -