カラツバ法で似非ゴースト暗算
| プログラムメモ | 2012/04/15 Sun 17:13
ゴースト暗算より早い!...場合もある計算方法....(汗
ゴースト暗算というのを、少し前に知りました。
ゴースト暗算が筆算であるなら、乗算4回・加算3〜4回の演算になります。
例えば、48x53を考えてみると
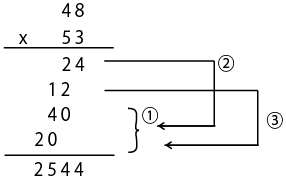
【通常の筆算】
4 8
x 5 3
---------
2 4
1 2
4 0
2 0
---------
2 5 4 4
【ゴースト暗算】
千の位と一の位を先に出して、残りを後から加算します。
通常の筆算の加算の順序を入れ替えていることがわかります。
(詳しくは書籍をご覧ください。魚の絵を使ったわかりやすいものです)
① (4x5)x10 + 8x5 = 240 ...千の位(2)
② 40x10 + 8x3
= 424 ...一の位(4)
③ 42 + 4x3 ...正確には一の位と十の位で分解して加算します
= 54
-----------------------------
2544
【カラツバ】
それならばと、ゴーストっぽいカラツバ法を考えてみました。
とは言っても単純に 基数を10 にしただけですが。
同様に千の位と一の位を先に出して、残りを後から計算します。
① (4x5)x100 + (8x3) = 2024 上位桁同士の乗算と下位桁同士の乗算なので繰り上がりはない。並べるだけ。
② (4x5) + (8x3) = 44 ①の上位部分と下位部分の加算。20+24+2
------------------------------
46
③ -(4-8)x(5-3) = 8 カラツバ法のミソ。
------------------------------
54
------------------------------
2544
上の説明ではわかりにくいので、計算方法を簡単なパターンにします。
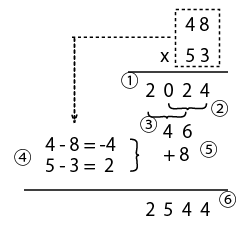
①上位桁と下位桁同士を掛けて並べます。(→2024)
②下3桁を足します(0+2+4→6)
③上3桁を足します(2+0+2→4)
...ここで元の十の位と一の位の数「0,2」は忘れて、2464を記憶する。
④掛ける数、掛けられる数、それぞれ十の位と一の位の差を取って掛けます。(-4x2→-8)
⑤符号反転(-8→+8)
⑥ ③と②でできた数に、⑤の数を足します。(46+8→54)
併せて繋げると、2544の出来上がり。
④がカラツバ法のミソで、たすき掛けの掛け算(4x3,8x5)は必要ありません。
いくつか計算サンプルを並べます。
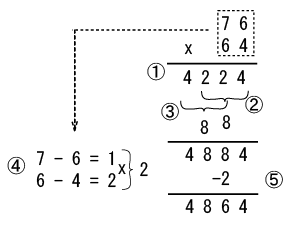
これもカラツバの効果が良く出ています。
最も効果が出るのは、十と一の位が同じ数字の場合で、
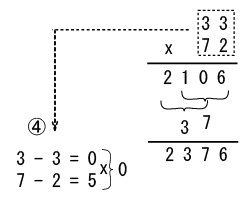
簡単すぎて驚きます。
残念ながら全ての数字の並びで簡単ではありません。
次の例をご覧ください。
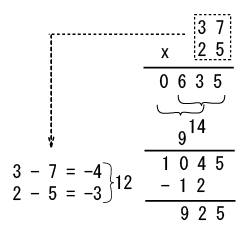
この例だと、桁上げと桁下げが発生するので、少し面倒です。
カラツバ法について詳しくは
http://ja.wikipedia.org/wiki/%E3%82%AB%E3%83%A9%E3%83%84%E3%83%90%E6%B3%95
一般には、分割統治法として有名で、乗算の他にも除算や平方根の多倍長数計算で使われます。(注)
Karatsuba博士 もこんな使い方されるとは、思わなかったでしょう。
【まとめ】
幾つかの例では、カラツバ法の方が早いような気もしますが、
ゴースト暗算の良さは、単純化された小さな加算を組み合わせることで、小学校低学年でも計算できるところにあります。
パターンによって難易度があまり上下するのは、低学年では厳しいかもしれません。
カラツバ法の場合、乗算回数が減りますが⑤⑥が減算になる場合もあるのでここが暗算上の鬼門になります。
例えば、乗数や被乗数に22や77など、同じ数字が並んでいる場合は④⑤がいらなくなるので簡単ですが、最後の例などカラツバ暗算で解くのは減算による桁下げがあるので面倒です。
また、小さな桁数であれば人間にとっては、加算より乗算の方が早いので、
本来のカラツバ法の効果は、全くと言っていい程ありません。(注)
2桁2桁までしか通用しないとか「そろばん」の方が良いとか批判的な意見も散見しますが、
ゴースト暗算は、イメージ(魚パターン)で簡単にわかりやすく計算方法を解説したという点では、
今までなかった新しい試みであり、ちょっと真似してみたくなりました。
どうでも良いことですが、どこのページも「48 x 53」を参考にしているので、
48x53の答えだけは覚えちゃっている人がいるのではないだろうか。
Tags: プログラムメモ
(注) Karatusba乗算について
ある基数の1次式で表現可能な2つの数の積は、この基数の2次式で計算でき、
加減算が増えても良ければ乗算3回で計算できる。
この3回の乗算で用いられる係数は、より小さな基数の1次式で表現できる。
それぞれの乗算をより小さな基数の2次式で表現する。
これを繰り返すことで、大きな数の乗算でも、小さな数の乗算に置き換えることがでます。
つまり、非常にコストが高い大きな数の乗算を、複数回の小さな数の乗算に変えることができます。
例えば、コストの掛らない小さな数を10進1桁として、4桁同士の乗算を行う場合、
まず、2桁の乗算3回に分割できる。
更にそれぞれの乗算係数をもう1回分割すれば、1桁の乗算9回(3x3)に分割できる。
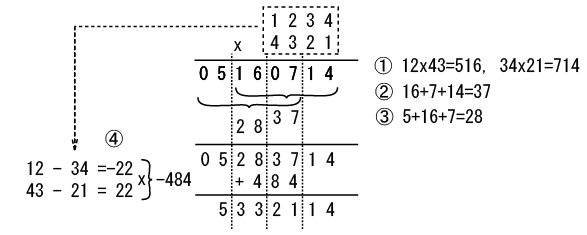
上記のように、まず2桁で区切って同じように計算を始めます。
①の段階で2桁x2桁の乗算が2回行われますので、1桁乗算だと3x2=6回。
④で2桁x2桁の乗算が1回なので、1桁乗算は併せて9回になります。
これを暗算で解くのはちょっと無理ですね。
コンピュータの場合であれば、数万Bitの大きな数の積でも、
大量に分割すれば、32bitの乗算で計算できることを示しています。
一般に計算機上では、再帰(Recursive)という方法でこれを実現します。
このように大きな問題を小さな問題に分割する方法や考え方を分割統治法といいます。
Karatusba法は基本的なアルゴリズムとして様々な書籍にも載っていますが、
この論文が発表されたのが1962年ですから、
現在だと、CPUよりメモリに関する計算コストが高いように思います。
個人的に作成した、乗算でカラツバ法を利用した多倍長整数電卓です。
整数だけですがおよそ100万桁まで計算できます。
author : HUNDREDSOFT | - | -